数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
"
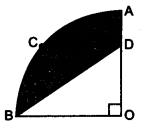
已知：正方形 OABC 内接于四分之一圆 OPBQ。$OA=20\ cm$。求解：我们需要求阴影部分的面积。解：$OABC$ 是一个正方形，且 $OA=AB=BC=CA=20\ cm$连接 $OB$。在 $\vartriangle OAB$ 中，$OB^{2} =OA^{2} +AB^{2}$$\Rightarrow \ OB^{2} =20^{2} +20^{2}$$\Rightarrow OB^{2} =400+400$$\Rightarrow OB=\sqrt{800}$$\Rightarrow OB=20\sqrt{2}$这里，$OB$ 是给定四分之一圆的半径 $r$。给定四分之一圆的面积 $A_{1} =\frac{\theta }{360^{o}} \times \pi r^{2}$$A_{1} =\frac{90^{o}}{360^{o} } \times 3.14\times \left( 20\sqrt{2}\right)^{2}$$\Rightarrow A_{1} =\frac{1}{4} \times 3.14\times 800$$\Rightarrow A_{1} =628cm^{2}$正方形的面积 $A_{2} =( 边长)^{2}$$\Rightarrow A_{2} =20\times 20$$\Rightarrow A_{2} =400cm^{2}$阴影部分的面积，$A=$四分之一圆的面积，$A_{1} -$正方形的面积，$A_{2}$$A=628-400$$\Rightarrow A=228cm^{2}$因此，面积 ... 阅读更多
"
已知：OACB 是一个以 O 为圆心，半径为 3.5 cm 的圆的四分之一圆。$OD = 2\ cm$求解：我们需要求阴影部分的面积。解：$OD = 2\ cm$$OB = 3.5\ cm$因此，三角形 $\mathrm{OBD}$ 的面积 $=\frac{1}{2} \times \mathrm{OB} \times \mathrm{OD}$$=\frac{1}{2} \times 3.5 \times 2$$=3.5 \mathrm{~cm}^{2}$阴影部分的面积 $=$ 四分之一圆的面积 $-$ 三角形 $\mathrm{OBD}$ 的面积$=\frac{77}{8}-\frac{35}{10}$$=\frac{77}{8}-\frac{7}{2}$$=\frac{77-28}{8}$$=\frac{49}{8} \mathrm{~cm}^{2}$阴影部分的面积是 $\frac{49}{8} \mathrm{~cm}^{2}$。
已知：OACB 是一个以 O 为圆心，半径为 3.5 cm 的圆的四分之一圆。$OD = 2\ cm$求解：我们需要求(i) 四分之一圆 OACB 的面积。(ii) 阴影部分的面积。解：(i) 四分之一圆 $OACB$ 的半径 $= 3.5\ cm$四分之一圆 $\mathrm{OACB}$ 的面积 $=\frac{\pi r^{2} \theta}{360^{\circ}}$$=\frac{22}{7} \times \frac{3.5 \times 3.5 \times 90^{\circ}}{360^{\circ}}$$=\frac{22 \times 35 \times 35 \times 90^{\circ}}{7 \times 360^{\circ} \times 100}$$=\frac{77}{8} \mathrm{~cm}^{2}$四分之一圆 OACB 的面积是 $\frac{77}{8} \mathrm{~cm}^{2}$。(ii) $OD = 2\ cm$$OB = 3.5\ cm$因此，三角形 $\mathrm{OBD}$ 的面积 $=\frac{1}{2} \times \mathrm{OB} \times \mathrm{OD}$$=\frac{1}{2} \times 3.5 \times 2$$=3.5 \mathrm{~cm}^{2}$阴影部分的面积 $=$ 四分之一圆的面积 $-$ ... 阅读更多
"
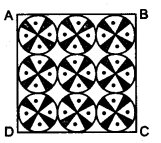
已知：在一块方形手帕上，制作了九个半径为 7 cm 的圆形图案。求解：我们需要求手帕剩余部分的面积。解：一个圆形图案的半径 $= 7\ cm$一个圆形图案的面积 $= \pi r^2$$= \frac{22}{7} \times 7^2$$= 154\ cm^2$9 个圆形图案的面积 $= 9 \times 154$$= 1386\ cm^2$圆形图案的直径 $= 7 \times 2$$= 14\ cm$正方形的边长 $= 3\times$ 一个圆的直径$= 3 \times 14$$= 42\ cm$正方形的面积 $= 42 \times 42$$= 1764\ cm^2$手帕剩余部分的面积 $=$ 正方形的面积 $-$ ... 阅读更多
"
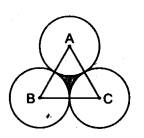
已知：等边三角形 ABC 的面积为 $17320.5\ cm^2$。以三角形的每个顶点为圆心，作一个半径等于三角形边长一半的圆。求解：我们需要求阴影部分的面积。解：等边三角形 $ABC$ 的面积 $= 17320.5\ cm^2$设三角形 $ABC$ 的边长为 $a$这意味着，$\triangle ABC$ 的面积 $= \frac{\sqrt3}{4}a^2$$\frac{\sqrt3}{4}a^2= 17320.5$$ a^{2} =\frac{17320.5 \times 4}{\sqrt{3}}$$a^{2}=\frac{17320.5 \times 4}{1.73205}$$a^{2}=40000$$a=200 \mathrm{~cm}$每个顶点所作圆的半径 $=\frac{1}{2} \text { (等边三角形的边长) }$$=\frac{1}{2} \times 200$$=100 \mathrm{~cm}$扇形面积 ... 阅读更多
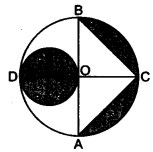
已知：AB 和 CD 是一个圆（圆心为 O）的两条互相垂直的直径，OD 是较小圆的直径。$OA = 7\ cm$。求解：我们需要求阴影部分的面积解：AB 和 CD 是圆心为 O 的圆的直径。圆的半径 $OA=OB=OC=OD=7\ cm$直径为 $AB$ 的圆的面积$=2\pi r^{2}$$=2\times \frac{22}{7} \times 7\times 7$$=308\ cm^{2}$另一个阴影圆的直径为 $OB=7\ cm$阴影圆的半径$=\frac{7}{2}\ cm$直径为 $OB$ 的阴影圆的面积$=\pi r^{2}$$=2\times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}$$=\frac{77}{2} \ cm^{2}$$\vartriangle ACD$ 的面积$=\frac{1}{2} \times ... 阅读更多
**已知：**如图所示，一个跑道的左右两端为半圆形。两条内平行线段之间的距离为 60 米，每条线段长 106 米。跑道宽 10 米。**求：**（i）沿着跑道内边缘的距离。（ii）跑道的面积。**解：**（i）两侧半圆形的周长 = $\frac{2 \pi r}{2}$ = $\pi r$两侧圆形半径 $r=\frac{60}{2}$ = 30 cm两侧半圆形的周长 = $\frac{22}{7} \times 30$ = $\frac{660}{7}$ cm半圆形总长度 = $\frac{2 \times 660}{7}$ = $\frac{1320}{7}$ cm内跑道的总长度 ... 阅读更多
"
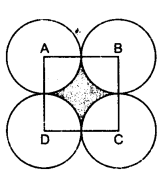
**已知：**ABCD 是边长为 14 厘米的正方形。以 A、B、C 和 D 为圆心，画四个圆，使得每个圆都与其余三个圆中的两个圆外切。**求：**阴影部分的面积。**解：**正方形 ABCD 的边长 = 14 cm这意味着，每个圆的半径 $r= 7\ cm$因此，阴影部分的面积 = 正方形的面积 - 正方形内四个扇形的面积$=(14)^{2}-4 \times \frac{1}{4} \pi 7^{2}$$=(14)^{2}-\frac{22}{7} \times 7^2$$=196-154$$=42 \mathrm{~cm}^{2}$阴影部分的面积为 $42\ cm^2$。
"
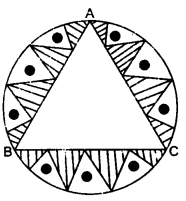
**已知：**在一个半径为 32 厘米的圆形桌布上，形成一个设计，中间留有一个等边三角形 ABC。**求：**设计的面积。**解：**圆的半径 $r=32 \mathrm{~cm}$设 AD 为△ABC 的中线，O 为圆心。$AO=\frac{2}{3}AD$$32=\frac{2}{3}AD$这意味着，$A D=48 \mathrm{~cm}$在△ABD 中，$A B^{2}=A D^{2}+BD^{2}$$A B^{2}=(48)^{2}+(\frac{A B}{2})^{2}$$(AB)^2-\frac{A B^{2}}{4}=(48)^{2}$$\frac{3AB^2}{4}=48\times48$$AB=\frac{48 \times 2}{\sqrt{3}}$$=\frac{96}{\sqrt{3}}$$=32 \sqrt{3}\ cm$等边三角形△ABC 的面积 = $\frac{\sqrt{3}}{4}(32 \sqrt{3})^{2}$$=\frac{\sqrt{3}}{4} \times 32 \times 32 \times 3$$=768 \sqrt{3} \mathrm{~cm}^{2}$圆的面积 = $\pi r^{2}$$=\frac{22}{7} \times(32)^{2}$$=\frac{22}{7} \times 1024$$=\frac{22528}{7} \mathrm{~cm}^{2}$设计的面积 = 圆的面积 - ... 阅读更多
"
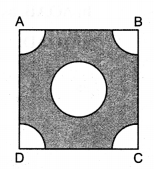
**已知：**从边长为 4 厘米的正方形的每个角上剪去一个半径为 1 厘米的圆的四分之一，并剪去一个直径为 2 厘米的圆。**求：**正方形剩余部分的面积。**解：**正方形 ABCD 的边长 = 4 cm正方形 ABCD 的面积 = 4^2 = 16 cm^2每个角上四分之一圆的半径 = 1 cm每个角上四分之一圆的面积 = $\frac{\pi r^{2} \theta}{360^{\circ}}$ = $\frac{22}{7} \times \frac{1 \times 1 \times 90^{\circ}}{360^{\circ}}$ = $\frac{22}{28} \mathrm{~cm}^{2}$四个角上的四个扇形的面积 = $\frac{4 \times 22}{28}$ = $\frac{22}{7} \mathrm{~cm}^{2}$ ... 阅读更多