$(i)$. 在 A 和 C 区域,磁场最大。$(ii)$. 在 B 区域,磁场最小。很明显,A 和 C 具有最多的磁场线,这些磁场线决定了磁场的强度,因为 A 和 C 是磁极,而 B 部分位于磁铁的中心,因此它没有磁场线。因此,B 附近磁场的强度几乎为零。
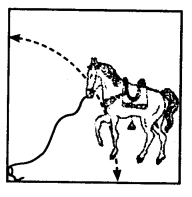
已知:一匹马用一根 5 米长的绳子系在一块边长为 15 米的正方形草地的一个角上的桩子上。要求:我们必须找到如果绳子长 10 米而不是 5 米,放牧面积的增加量。解答:绳子的长度从 5 米增加到 10 米这意味着,马放牧的新扇形半径 = 10 米因此,马放牧的面积 = 象限面积 (10 米)=$\frac{1}{4}\pi r^2$$=\frac{1}{4}\times3.14\times(10)^2$$=25\times3.14$$=78.5\ m^2$这意味着,放牧面积的增加量 = 78.5 - 19.625 = 58.875 平方米因此,放牧面积的增加量 ... 阅读更多
已知:半径为 10 厘米的圆的弦在圆心处张成一个直角。要求:我们必须找到相应优扇形的面积。解答:因为圆的半径 = OA = OB = 10 厘米弦张成的角 = ∠AOB = θ = 90 度优扇形的面积 = 圆的面积 - 劣扇形的面积= π r^2 - $\frac{\pi\theta}{360^{\circ}}\times OA\times OB$$=3.14\times10\times10-3.14\times\frac{90^{\circ}}{360^{\circ}}\times10\times10$$=314-78.5$$=235.5\ cm^2$因此,优扇形的面积为 235.5 平方厘米。
已知:圆的半径 $r=21 \mathrm{~cm}$。弧所张成的角 $=60^{\circ}$要求:我们必须找到 (i) 弧长。(ii) 弧所形成的扇形的面积。(iii) 由相应的弦形成的弓形的面积。解答:(i) 令弧长为 $l$。我们知道,弧长 $=2 \pi r(\frac{\theta}{360^{\circ}})$因此,弧长 $l=2 \times \frac{22}{7} \times 21 \times \frac{60^{\circ}}{360^{\circ}} \mathrm{cm}$$=132 \times \frac{1}{6} \mathrm{cm}$$=22 \mathrm{cm}$弧长为 22 厘米。 (ii) 我们知道,扇形的面积 $=\pi r^{2} \times \frac{\theta}{360^{\circ}}$因此,弧所形成的扇形的面积=$\frac{22}{7}(21)^{2} \times \frac{60^{\circ}}{360^{\circ}}$$=\frac{22}{7} \times 21 \times ... 阅读更多
已知:圆的半径 $r=21 \mathrm{~cm}$。弧所张成的角 $=60^{\circ}$要求:我们必须找到扇形的面积。解答:我们知道,扇形的面积 $=\pi r^{2} \times \frac{\theta}{360^{\circ}}$因此,弧所形成的扇形的面积=$\frac{22}{7}(21)^{2} \times \frac{60^{\circ}}{360^{\circ}}$$=\frac{22}{7} \times 21 \times 21 \times \frac{1}{6}$$=231 \mathrm{~cm}^{2}$扇形的面积为 231 平方厘米。
已知:圆的半径 $r=21 \mathrm{~cm}$。弧所张成的角 $=60^{\circ}$要求:我们必须找到由相应的弦形成的弓形的面积。解答:我们知道,扇形的面积 $=\pi r^{2} \times \frac{\theta}{360^{\circ}}$因此,弧所形成的扇形的面积=$\frac{22}{7}(21)^{2} \times \frac{60^{\circ}}{360^{\circ}}$$=\frac{22}{7} \times 21 \times 21 \times \frac{1}{6}$$=231 \mathrm{~cm}^{2}$因此,由相应的弦形成的弓形的面积 = 扇形的面积 - 弦与圆的半径之间形成的三角形的面积$=231-(\frac{1}{2} r^{2} \sin \theta)$$=231-\frac{1}{2} \times(21)^{2} \times \sin 60^{\circ}$$=231-\frac{1}{2} \times 441 \times \frac{\sqrt{3}}{2}$$=231-\frac{441 \sqrt{3}}{4}$$=231-190.95$$=40.05 \mathrm{~cm}^{2}$由... 阅读更多
已知:半径为 15 厘米的圆的弦在圆心处张成 60 度角。要求:我们必须找到圆的相应劣弓形和优弓形的面积。解答:圆的半径 $r = 15\ cm$圆心角 θ = 60 度扇形的面积 = $\frac{\pi r^2 \theta}{360^o}$$= \frac{3.14 \times 15\times15\times60^o}{360^o}$$= 117.75\ cm^2$由半径和弦形成的三角形的面积 = $\frac{1}{2}r^2 \theta$$= \frac{1}{2}(15)^2\ sin\ 60^o$$= \frac{1}{2} \times 225 \times \frac{\sqrt3}{2}$$= 97.31\ cm^2$劣弓形的面积 = 扇形的面积 - 由半径和弦形成的三角形的面积$= 117.75 - ... 阅读更多
已知:半径为 12 厘米的圆的弦在圆心处张成 120 度角。要求:我们必须找到圆的相应弓形的面积。解答:假设有一个圆心为 O 的圆,AB 是给定的弦,如图所示。这里给定圆的半径,$r=12\ cm$弦 AB 所张成的角,∠AOB=120 度。扇形 AOB 的面积=$\frac{\theta }{360^{o}} \pi r^{2}$这里 θ=120 度,r=12 厘米=$\frac{120^{o}}{360^{o}} \times 3.14 \times ( 12)^{2}$$=\frac{1}{3} \times 3.14 \times 12\times 12$$=150.72 \ cm^{2}$扇形 AOB 的面积=150.72 平方厘米三角形 ABC 的面积=$\frac{1}{2} \times OA\times ... 阅读更多
已知:一匹马用一根 5 米长的绳子系在一个边长为 15 米的正方形草场的角上的桩子上。要求:我们必须找到 (i) 马可以吃草的草场部分的面积。(ii) 如果绳子长 10 米而不是 5 米,放牧面积会增加多少。解答:(i) 根据题意,马可以吃草的最大面积是一个半径为 r=5 米的圆的四分之一的面积。因此,马吃草的面积 = 四分之一圆的面积 ( ... 阅读更多
已知:圆的面积和周长在数值上相等。要求:我们必须找到圆的半径。解答:设圆的半径为 r。则圆的面积 = πr²圆的周长 = 2πr根据题意,圆的面积和周长在数值上相等。⇒ πr²=2πr⇒ r²=2πr/π⇒ r²=2r⇒ r=2 个单位因此,圆的半径为 2 个单位。选项 A 是正确答案。

 数据结构
数据结构 网络
网络 RDBMS
RDBMS 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP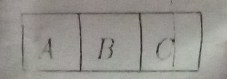

 "
"