数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
已知：一个等差数列前 7 项的和为 49，前 17 项的和为 289。求解：我们需要求出前 n 项的和。解：设首项为 a，公差为 d。我们知道，前 n 项和 Sn = n/2(2a + (n-1)d)S7 = 7/2[2(a) + (7-1)d]49 = 7/2(2a + 6d)49 = 7(a + 3d)a + 3d = 7a = 7 - 3d ......(i)S17 = 17/2[2(a) + (17-1)d]289 = 17/2(2a + 16d)289 = 17(a + 8d)a + 8d = 177 - 3d + 8d = 17 (根据 (i))5d = 17 - 7d = 10/5d = 2这意味着，a = 7 - 3(2)a = 7 - 6a = 1前 n 项和 Sn = n/2(2a + (n-1)d)Sn = n/2[2(1) + (n-1)2]= n(1 + n - 1)= n²因此，前 n 项的和为 n²。 阅读更多
求解：我们需要证明 $a_1, a_2, ……. a_n, ……$ 构成一个等差数列，并在每种情况下求出前 15 项的和。解：(i) 这里，$a_{n}=3+4 n$这意味着，$a_{1}=3+4 \times 1$$=3+4$$=7$$a=7$$a_{2}=3+4 \times 2$$=3+8$$=11$ $a_{3}=3+4 \times 3$$=3+12$$=15$ 这意味着，$d=a_{2}-a_{1}$$=11-7$$=4$因此，$a_1, a_2, ……. a_n, ……$ 构成一个等差数列项数 = 15我们知道，$S_{n}=\frac{n}{2}[2 a+(n-1) d]$$S_{15}=\frac{15}{2}[2 a+(15-1) d]$$=\frac{15}{2}[2 \times 7+(15-1) \times 4]$$=\frac{15}{2}[14+14 \times 4]$$=\frac{15}{2}[14+56]$$=\frac{15}{2} \times 70$$=15 \times 35$$=525$前 15 项的和是 $525$。 (ii) 为了找到给定的序列，我们必须在 $a_n=9-5n$ 中代入 $n=1, 2, 3.....$。因此，$a_1=9-5(1)$$=9-5$$=4$$a_2=9-5(2)$$=9-10$$=-1$$a_3=9-5(3)$$=9-15$$=-6$$a_4=9-5(4)$$=9-20$$=-11$形成的序列是 $4, -1, -6, -11, ... 阅读更多
已知：$a_n=9-5n$求解：我们需要证明 $a_1, a_2, ……. a_n, ……$ 构成一个等差数列，并求出前 15 项的和。解：为了找到给定的序列，我们必须在 $a_n=9-5n$ 中代入 $n=1, 2, 3.....$。因此，$a_1=9-5(1)$$=9-5$$=4$$a_2=9-5(2)$$=9-10$$=-1$$a_3=9-5(3)$$=9-15$$=-6$$a_4=9-5(4)$$=9-20$$=-11$形成的序列是 $4, -1, -6, -11, .....$。为了使给定序列构成一个等差数列，任何两个连续项之间的差都应该相等。这里，$d=a_2-a_1=-1-4=-5$$d=a_3-a_2=-6-(-1)=-6+1=-5$$d=a_4-a_3=-11-(-6)=-11+6=-5$这意味着，$a_2-a_1=a_3-a_2=a_4-a_3=d$因此，给定序列构成一个等差数列。 我们知道，$S_{n}=\frac{n}{2}[2 a+(n-1) d]$$S_{15}=\frac{15}{2}[2 a+(15-1) d]$$=\frac{15}{2}[2 \times 4+(15-1) \times (-5)]$$=\frac{15}{2}[8+14 \times (-5)]$$=\frac{15}{2}[8-70]$$=\frac{15}{2} \times (-62)$$=15 \times (-31)$$=-465$前 15 项的和是 $-465$。 阅读更多
已知：矩形长和宽如下：$(10m, 5n)$$(20x^2, 5y^2)$求解：我们需要求出矩形的面积。解：我们知道，长为 l，宽为 b 的矩形的面积为 lb。因此，长和宽分别为 $(10m, 5n)$ 的矩形的面积为，A = 10m × 5n = 50mn长和宽分别为 $(20x^2, 5y^2)$ 的矩形的面积为，A = 20x² × 5y² = 100x²y²
已知：一个等差数列前 n 项的和为 $4n-n^{2}$。求解：我们需要求出首项（即 $S_1$），前两项的和，第二项，第 3 项，第 10 项和第 n 项。解：$S_{n} =4n-n^{2}$当 n=1 时，$S_{1} =4\times 1 -1^2=4-1=3$因此，首项 a=3当 n=2 时，$S_{2} =4\times 2-2^{2}=8-4=4$因此，等差数列的第二项 = S₂ - S₁ = 4-3 = 1等差数列的公差 d = 第二项 - 首项 = 1-3 = -2我们知道，$a_{n}=a+(n-1)d$$a_{2}=a+d=3+(-2)=3-2=1$$a_3=a+2d=3+2(-2)=3-4=-1$$a_{10}=a+(10-1)d=3+9(-2)=3-18=-15$$a_n=a+(n-1)d=3+(n-1)(-2)$$=3-2n+2$$=5-2n$因此，首项为 3，第二项为 1，第三项为 -1，第十项为 -15，第 n 项为 5-2n，前两项的和为 ... 阅读更多
已知：前 40 个能被 6 整除的正整数。求解：我们需要求出前 40 个能被 6 整除的正整数的和。解：前 40 个 6 的倍数是 6,12,18,24, ..., 240这里，a=6, d=6 且 l=240Sn = n/2[2a + (n-1)d]S₄₀ = 40/2[2 × 6 + (40-1) × 6] = 20[12 + 39 × 6] = 20[12 + 234] = 20 × 246 = 4920前 40 个能被 6 整除的正整数的和是 4920。
已知：0 和 50 之间的奇数。求解：我们需要求出 0 和 50 之间的奇数的和。解：0 和 50 之间的奇数是 1,3,5,7, ..., 49。这个序列是等差数列。这里，a=1 且 d=3-1=2 l=49我们知道，l=a+(n-1)d49=1+(n-1) × 249=1+2n-249+1=2n n=50/2=25因此，n=25我们知道，Sn = n/2[2a + (n-1)d] = 25/2[2 × 1 + (25-1) × 2] = 25/2[2 + 24 × 2] = 25/2(50) = 25 × 25 = 6250 和 50 之间所有奇数的和是 625。
已知：一项建筑工程合同规定，如果完工时间超过规定的日期，则将按以下方式处以罚款：第一天 200 卢比，第二天 250 卢比，第三天 300 卢比，依此类推，每天的罚款比前一天多 50 卢比。求解：我们需要求出如果承包商延误完工 30 天，他需要支付多少罚款。解：设第一天的罚款为 a₁，第二天的罚款为 a₂，依此类推，天数为 n。a₁=a=200, a₂=250d=a₂-a₁=250-200= 50n=30我们知道，Sn = n/2[2a + (n-1)d]因此，S₃₀ = 30/2[2 ... 阅读更多
已知：在一所学校里，学生们想到在学校内外种植树木来减少空气污染。他们决定每个班级的每个班的树木数量将与他们所学的年级相同，例如：一年级的每个班将种 1 棵树，二年级的每个班将种 2 棵树，以此类推，直到十二年级。每个年级都有三个班。求解：我们需要求出学生们将种植多少棵树。解：每个年级种植的树木数量如下：年级班树木数量 ... 阅读更多
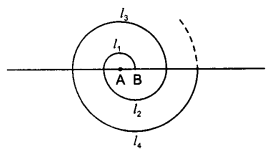
已知：一个螺旋形由连续的半圆组成，圆心交替位于 A 和 B 点，从 A 点开始，半径分别为 0.5 厘米、1.0 厘米、1.5 厘米、2.0 厘米……