数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
题目：我们必须证明等边三角形的条中线相等。解答：设在△ABC中，AD、BE和CF是三角形的条中线，且AB=BC=CA。在△BCE和△BCF中，BC=BC（公共边），CE=BF，∠C=∠B（等边对等角）。因此，根据SAS公理，△BCE≅△BCF。这意味着BE=CF……(i)同样，△CAD≅△CAF，这意味着AD=CF……(ii)由(i)和(ii)，AD=BE=CF。证毕。
已知：在△PQR中，PQ=QR，L、M和N分别是PQ、QR和RP的中点。题目：我们必须证明LN=MN。解答：在△LPN和△MRH中，PN=RN（因为M是PR的中点），LP=MR，∠P=∠R（等边对等角）。因此，根据SAS公理，△LPN≅△MRH。这意味着LN=MN（CPCT）。证毕。
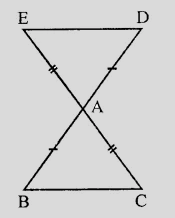
"\已知：边BA和CA已延长，使得BA=AD且CA=AE。题目：我们必须证明线段DE∥BC。解答：在△ABC和△DAE中，AB=AD（已知），AC=AE（已知），∠BAC=∠DAE（对顶角）。因此，根据SAS公理，我们得到△ABC≅△DAE。这意味着∠ABC=∠ADE（CPCT）。∠ABC和∠ADE是内错角。因此，DE∥BC。
已知：一个振动物体的时间周期为0.06秒。题目：找出这种声音能否被人耳探测到。解答：这里，如所给，时间周期T=0.06秒。因此，声音的频率f=1/T=1/0.06秒=16.67赫兹。这里，声音的频率太低，人耳无法听到。所以这种探测到的声音人耳听不到。
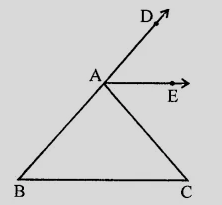
"\已知：AE平分∠CAD，且∠B=∠C。题目：我们必须证明AE∥BC。解答：在△ABC中，BA被延长。这意味着∠CAD=∠B+∠C。2∠EAC=∠C+∠C（因为AE是∠CAE的平分线）。2∠EAC=2∠C。∠EAC=∠C。∠EAC和∠C是内错角。这意味着AE∥BC。证毕。
已知：在△ABC中，BD⊥AC，CE⊥AB。BD和CE相交于O。题目：我们必须证明∠BOC=180°-∠A。解答：从图中，在四边形ADOE中，∠A+∠D+∠O+∠E=360°（四边形内角和）。∠A+90°+∠DOE+90°=360°。∠A+∠DOE=360°-180°=180°。∠BOC=∠DOE（对顶角）。这意味着∠A+∠BOC=180°。∠BOC=180°-∠A。证毕。
"\已知：AM⊥BC，AN是∠A的平分线。∠B=65°，∠C=33°。题目：我们必须求∠MAN。解答：AM⊥BC，这意味着∠AMC=90°。∠AMN=90°。在△ABC中，∠A+∠B+∠C=180°。∠A+65°+33°=180°。∠A+98°=180°。∠A=180°-98°=82°。AN是∠A的平分线。这意味着∠NAC=∠NAB=1/2∠A=1/2×82°=41°。在△AMN中，∠ANM=∠C+∠NAC=33°+41°=74°。在△MAN中，∠MAN+∠AMN+∠ANM=180°。∠MAN+90°+74°=180°。∠MAN+164°=180°。∠MAN=180°-164°。∠MAN=16°。因此，∠MAN=16°。阅读更多
已知：在△ABC中，AD平分∠A，且∠C＞∠B。题目：我们必须证明∠ADB＞∠ADC。解答：在△ABC中，AD是∠A的平分线。这意味着∠1=∠2。在△ADC中，∠ADB=∠1+∠C。∠C=∠ADB-∠1……(i)同样，在△ABD中，∠ADC=∠2+∠B。∠B=∠ADC-∠2……(ii)∠C＞∠B。由(i)和(ii)，我们得到(∠ADB-∠1)＞(∠ADC-∠2)。∠1=∠2。因此，∠ADB＞∠ADC。证毕。
已知：ABC是一个三角形。B处的外部角平分线和∠C的平分线相交于D。题目：我们必须证明∠D=1/2∠A。解答：在△ABC中，CB延长到E。∠ABE和∠ACB的平分线在D处相交。在△BDC中，∠ABE=∠A+∠C。1/2∠ABE=1/2∠A+1/2∠C。∠1=1/2∠A+∠4……(i)在△BDC中，∠2=∠D+∠4。∠D=∠2-∠4=∠1-∠4=(1/2∠A+∠4)-∠4 [来自(i)]=1/2∠A+∠4-∠4=1/2∠A。因此，∠D=1/2∠A…阅读更多
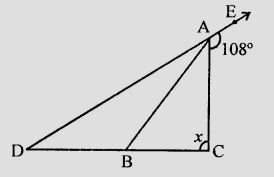
"\已知：$AB$ 将 $\angle DAC$ 按比例 $1:3$ 分割，且 $AB = DB$。求：$x$ 的值。解：$\angle CAE + \angle DAC = 180^{\circ}$ (邻补角)$108^{\circ} + \angle DAC = 180^{\circ}$$\angle DAC = 180^{\circ} - 108^{\circ}$$= 72^{\circ}$$\angle DAB = 72^{\circ} \times \frac{1}{1+3}$$=\frac{72^{\circ} \times 1}{4}$$= 18^{\circ}$$\angle CAB = 72^{\circ} \times \frac{3}{4}$$= 54^{\circ}$等边对等角。这意味着 $\angle DAB = \angle ADB = 18^{\circ}$ (因为 $AB = DB$)在 $\triangle ADC$ 中，$\angle CAE = \angle BDA + \angle ACD$$108^{\circ} = 18^{\circ} + x$$x = 108^{\circ} - 18^{\circ}$$= 90^{\circ}$$x$ 的值为 $90^{\circ}$。阅读更多