已知:如图所示,从外一点 P 引出切线 PQ 和 PR 到圆心为 O 的圆,使得∠RPQ=30°。一条弦 RS 平行于切线 PQ。求解:我们需要求∠RQS。解:PQ 和 PR 是从 P 点引出的圆心为 O 的圆的切线,且∠RPQ = 30°。RS ∥ PQ。PQ = PR (从外一点引出的圆的切线相等)∠PRQ = ∠PQR ∠…阅读更多
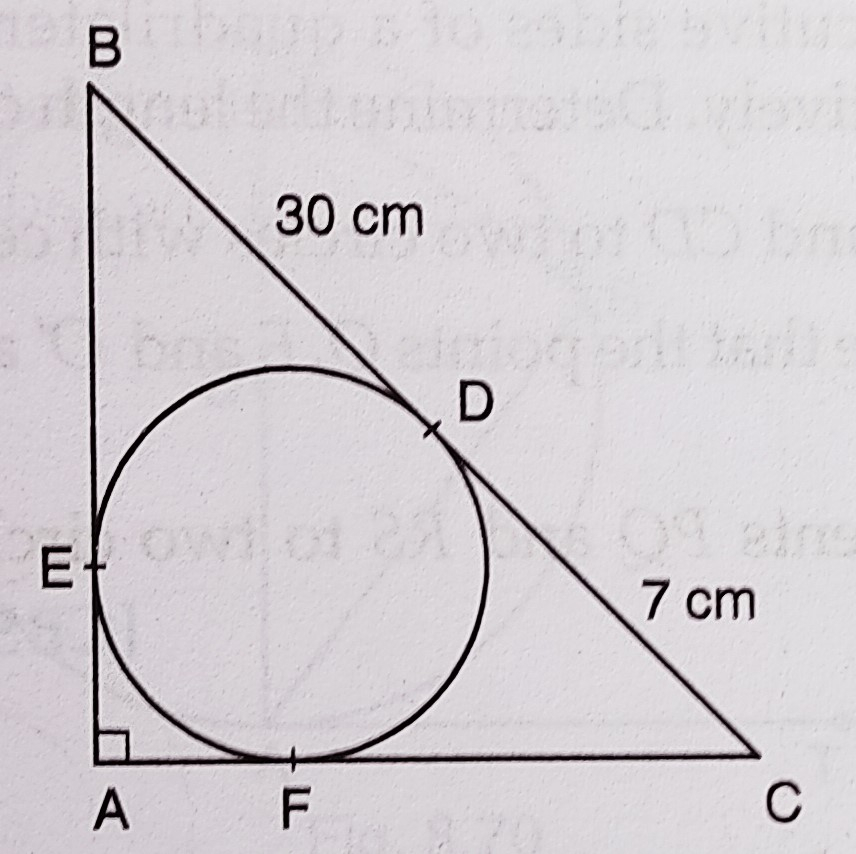
已知:如图所示,BDC 是在点 D 与给定圆相切的切线,使得 BD=30 cm 和 CD=7 cm。其他切线 BE 和 CF 分别从 B 和 C 引出到圆,并在 A 点相交,构成直角三角形 BAC。求解:我们需要计算 AF。解:AB、BC 和 AC 是在 E、D 和 F 点与圆相切的切线。BD = …阅读更多
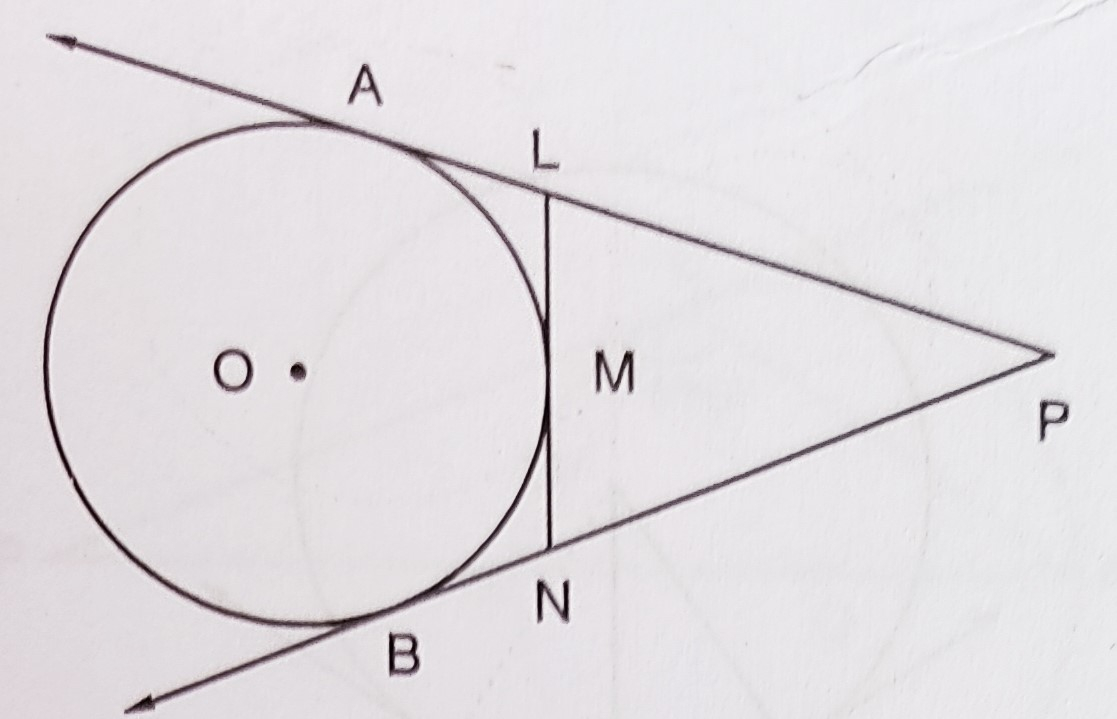
已知:如图所示,PA 和 PB 是从外一点 P 到圆心为 O 的圆的切线。LN 在 M 点与圆相切。求解:我们需要证明 PL+LM=PN+MN。解:PA 和 PB 是从 P 点引出的圆的切线。这意味着,PA = PB 同样,LA 和 LM 是从 L 点引出的切线。LA = LM NB = NM 因此,PA = PB ⇒ PL + LA = PN + NB PL + LM = PN + NM 证毕。
已知:如图所示,AB 是半径为 10 cm 的圆的一条长为 16 cm 的弦。A 和 B 处的切线在一个点 P 相交。求解:我们需要求 PA 的长度。解:连接 OA。OA = 10 cm OL 垂直于 AB。AL=LB= 16/2=8 cm (AL 和 LB 是圆的半径)在直角三角形 OLA 中,根据毕达哥拉斯定理,OA²=OL² +LA² OL²=OA²-LA² OL²=(10)²-8² =100-64 =36 ⇒ OL=6 cm tan∠AOL=AL/OL =8/6 =4/3 从△OAP,tan∠AOL=PA/OA 4/3=PA/10 PA=(10×4)/3 PA=40/3 cm PA 的长度为 40/3 cm。阅读更多
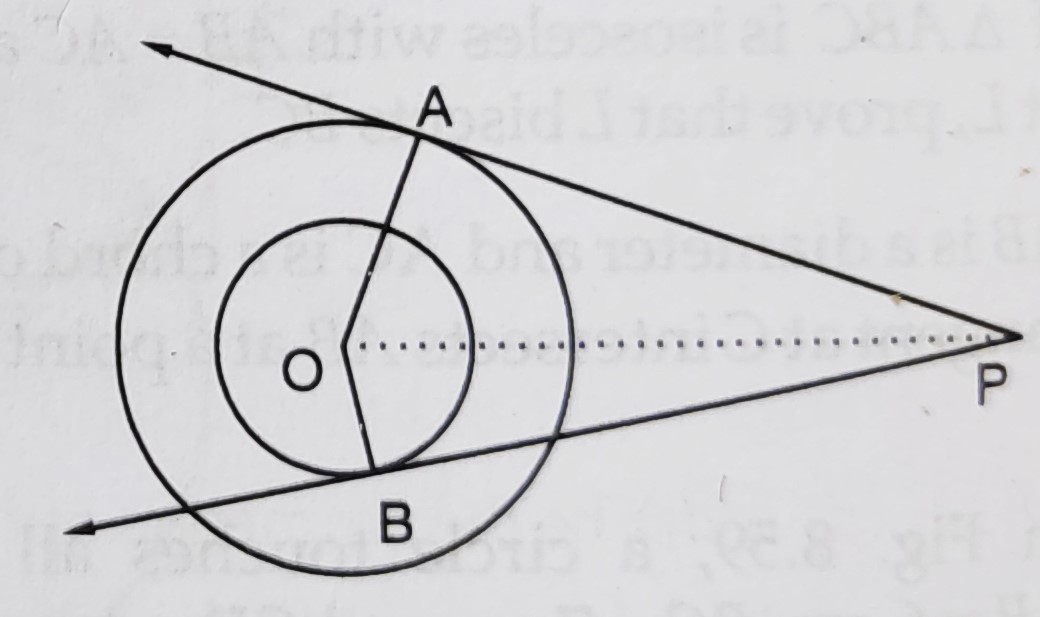
已知:如图所示,有两个同心圆,圆心为 O,半径分别为 5 cm 和 3 cm。从外一点 P,引出切线 PA 和 PB 到这两个圆。AP=12 cm。求解:我们需要求 BP 的长度。解:从图中,AP = 12 cm 在直角三角形 OAP 中,根据毕达哥拉斯定理,OP² = OA² + AP² = 5² + (12)² = 25 + 144 = 169 = (13)² ⇒ OP = 13 cm 在直角三角形 OBP 中,OP² = OB² + BP² (13)² = 3² + BP² 169 = 9 + BP² BP² = 169 - 9 = 160 = 16 × 10 ⇒ BP = √(16 × 10) = 4√10 cm BP 的长度是 4√10 cm。
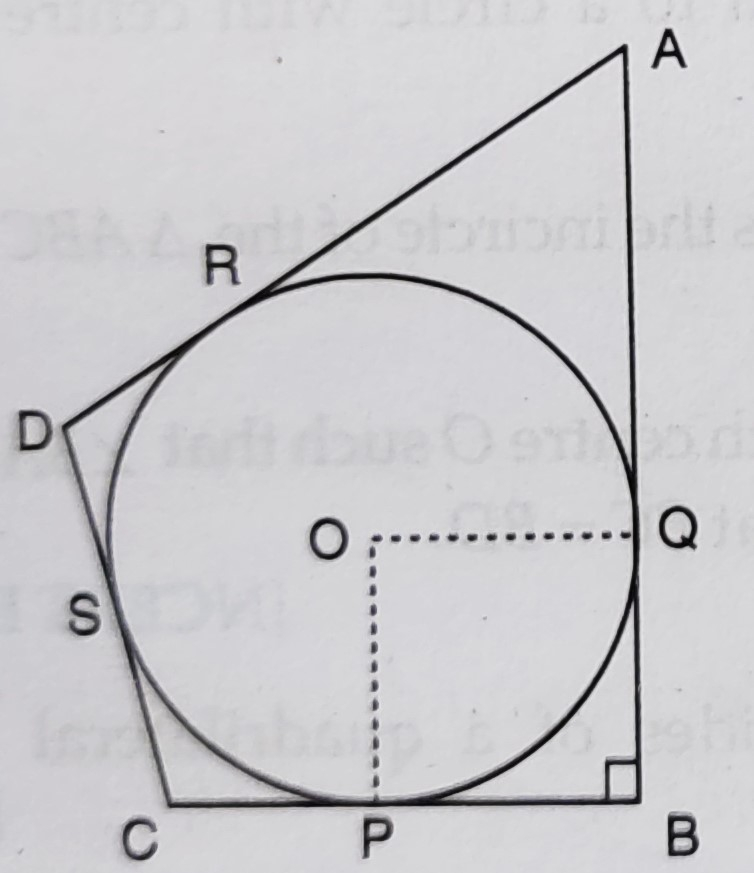
已知:如图所示,一个圆内接于一个四边形 ABCD,其中∠B=90°。AD=23 cm,AB=29 cm,DS=5 cm。求解:我们需要求圆的半径 r。解:从图中,OQ=OP=r AB 和 BC 是圆的切线,OP 和 OQ 是圆的半径。OP ⊥ BC 和 OQ ⊥ AB ∠OPB = ∠OQB = 90° PBQO 是一个正方形。DS 和 DR 是圆的切线。这意味着,DR = DS = 5 cm AR = AD - DR = 23 …阅读更多
已知:有理数:12/7 和 3/7。求解:计算给定有理数的和。解:给定的分数是:12/7 和 3/7。相加后,12/7+3/7 = (12+3)/7 =15/7。
自然数用 N 表示。整数用 W 表示。
已知:三个数的比例为 2:3:4。它们的立方和是 33957。求解:求这些数。解:设这些数为 2x、3x 和 4x。立方和=33957 ⇒ (2x)³ + (3x)³ + (4x)³=33957 ⇒ 8x³ + 27x³ + 64x³=33957 ⇒ 99x³=33957 ⇒ x³=33957/99=343 ⇒ x=∛343=7 这些数是:2x=2×7=14 3x=3×7=21 4x=4×7=28 因此,这些数是:14、21、28。
已知:多项式:$f( x)=x^{2}-9 x+20$

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP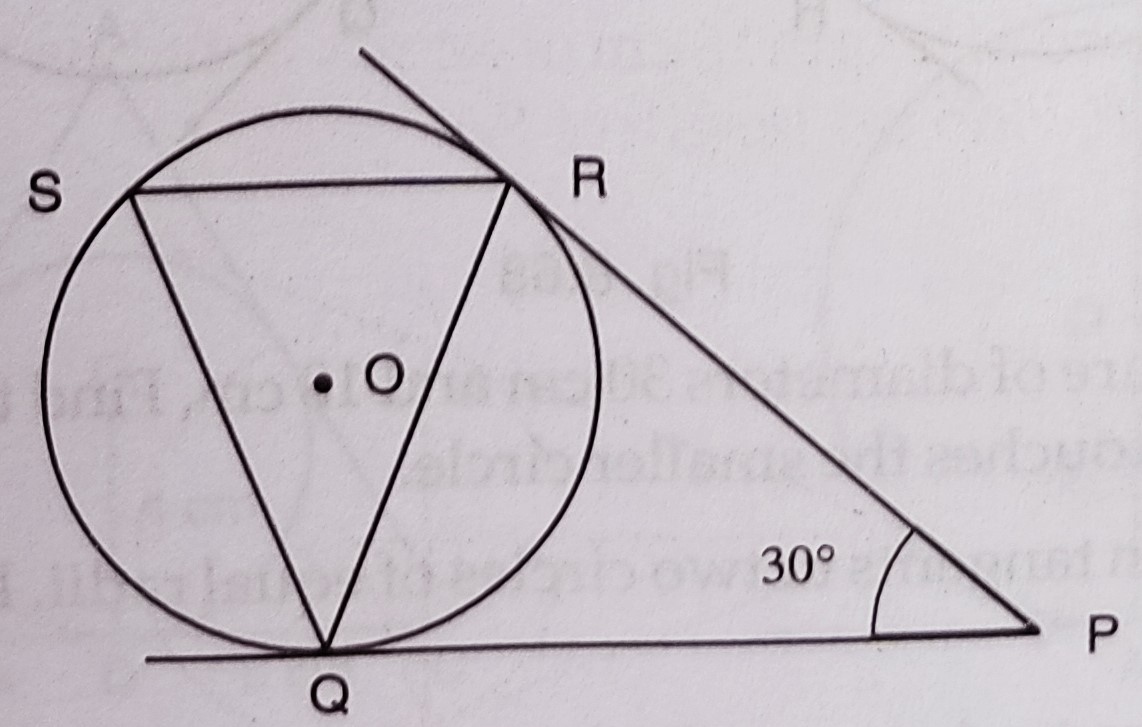 "\
"\
 "\
"\ "\
"\ "\
"\ "\
"\ "\
"\