数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
已知：一座塔的影子落在水平地面上，当太阳高度角为 $30^{\circ}$ 时比太阳高度角为 $60^{\circ}$ 时长 $40\ m$。求解：求塔的高度。解：当太阳高度角为塔顶到影子顶端的仰角时。设 $AB$ 为 $h\ m$，$BC$ 为 $x\ m$。根据题意，$DB$ 比 $BC$ 长 $40\ m$。所以，$BD=( 40+x)\ m$ 并且形成了两个直角三角形 $ABC$ 和 $ABD$。在 $\vartriangle ABC$ 中，$tan\ 60^o=\frac{AB}{BC}$$\Rightarrow \sqrt{3}=\frac{h}{x}$$\Rightarrow x=\frac{h}{\sqrt{3}}$ ........ $( i)$在 $\vartriangle ABD$ 中，$\Rightarrow tan\ 30^o=\frac{AB}{BD}$$\Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{( x+40)}$$\Rightarrow x+40=\sqrt{3}h$ $\Rightarrow \frac{h}{\sqrt{3}+40}=\sqrt{3}h$ ... 阅读更多
已知：画一个三角形 \( P Q R \) 外接半径为 \( 8 \mathrm{~cm} \) 的圆，使得 \( Q R \) 被切点 \( T \) 分成的线段 \( Q T \) 和 \( T R \) 的长度分别为 \( 14 \mathrm{~cm} \) 和 \( 16 \mathrm{~cm} \)。\( \Delta P Q R \) 的面积为 \( 336 \mathrm{~cm}^{2} \)。求解：我们需要求边 \( P Q \) 和 \( P R \) 的长度。解：$\triangle PQR$ 外接以 $O$ 为圆心，半径为… 阅读更多
已知：两个同心圆的直径分别为 \( 30 \mathrm{~cm} \) 和 \( 18 \mathrm{~cm} \)。求解：我们需要求外圆的弦长，该弦与内圆相切。解：设外圆的半径为 $R$，内圆的半径为 $r$。$AB$ 是外圆的弦，在 $P$ 点与内圆相切。连接 $OP$ 和 $OA$。这意味着，$OP\ \perp\ AB$ 并且平分它于 $P$ 点。$OA=R$ 且 $OP=r$$OA=\frac{30}{2}=15\ cm$，$OP=\frac{18}{2}=9\ cm$在直角三角形 $OAP$ 中，$AP=\sqrt{OA^{2}-OP^{2}}$$=\sqrt{15^{2}-9^{2}}$$=\sqrt{225-81}$$=\sqrt{144}$$=12\ cm$$AB=2AP$$=2 \times 12\ cm$$=24\ cm$外圆弦的长度… 阅读更多
已知：\( A B \) 和 \( C D \) 是两个半径相等的圆的公切线。求解：我们需要证明 \( A B=C D \)。解：连接 $OA, OC, OB$ 和 $OD$。从图中，$\angle OAB = 90^o$ （圆上任意一点的切线垂直于过该点的半径）这意味着，$AC$ 是一条直线。$\angle OAB + \angle OCD = 180^o$$AB\ \parallel\ CD$类似地，$BD$ 是一条直线，且 $\angle OBA = ∠ODC = 90^o$$AC = BD$ （两个圆的半径相等）在四边形 $ABCD$ 中，$\angle A = \angle B ... 阅读更多
已知：两个圆的圆心分别为 \( O \) 和 \( O^{\prime} \)，它们的公切线 \( A B \) 和 \( C D \) 在它们的圆心之间相交于 \( E \)。求解：我们需要证明点 \( O, E \) 和 \( O^{\prime} \) 共线。解：连接 $OA$ 和 $OC$。在 $\triangle OAE$ 和 $\triangle OCE$ 中，$OA=OC$ （同一个圆的半径）$OE=OE$ （公共边）$\angle OAE=\angle OCE=90^{\circ}$$\Rightarrow \triangle OAE \cong \triangle OCE$ （根据 RHS 全等）$\Rightarrow \angle AEO=\angle CEO$ （对应边相等）类似地，$\angle BEO^{\prime}=\angle DEO^{\prime}$$\angle AEC=\angle DEB$$\Rightarrow \frac{1}{2} \angle AEC=\frac{1}{2} \angle DEB$$\Rightarrow \angle AEO=\angle CEO=\angle BEO^{\prime}=\angle ... 阅读更多
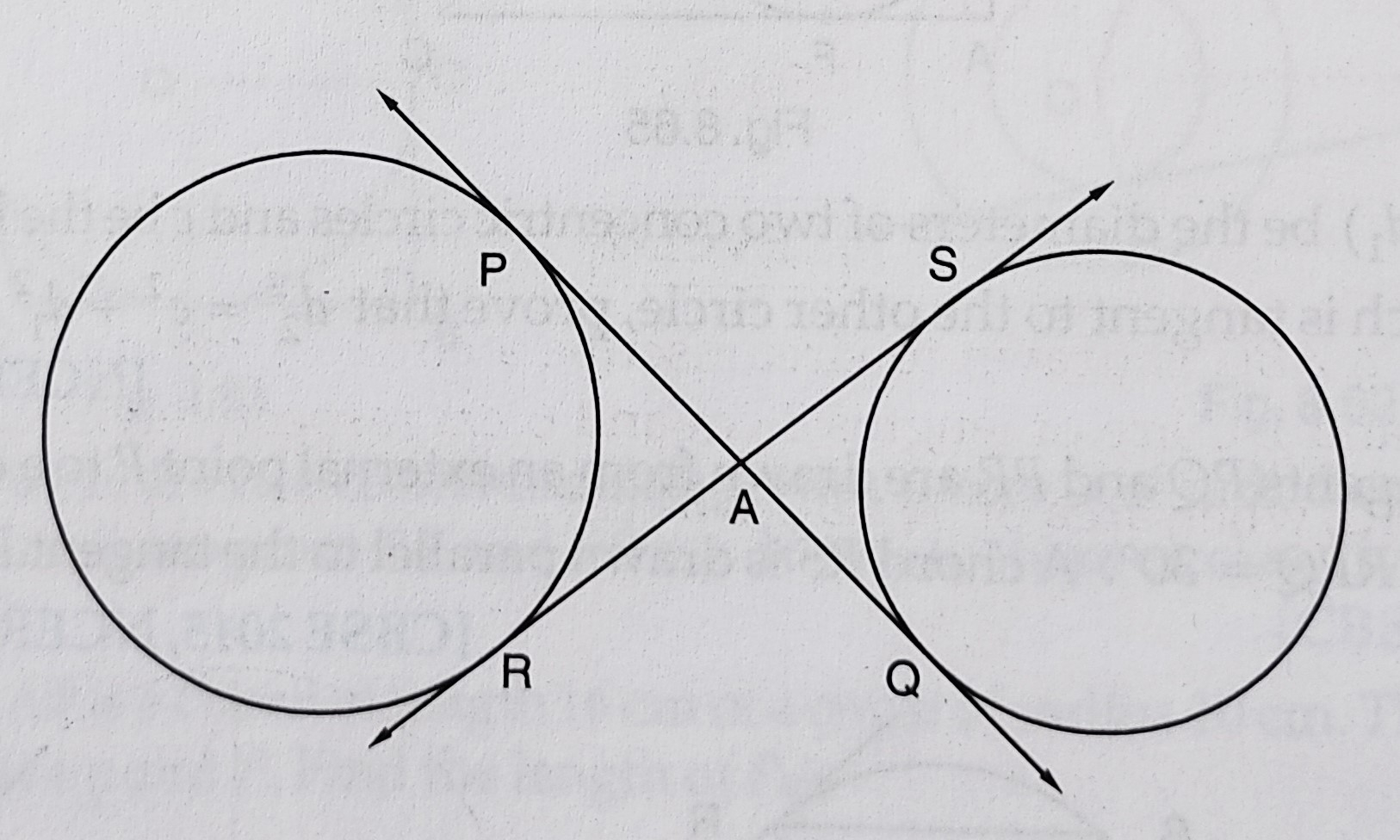
"\已知：如图所示，两个圆的公切线 \( P Q \) 和 \( R S \) 相交于 \( A \)。求解：我们需要证明 \( P Q=R S \)。解：$AQ$ 和 $AR$ 是从 $A$ 引向圆心为 $O$ 的圆的两条切线。$AP = AR$....….(i)类似地，$AQ$ 和 $AS$ 是圆心为 $C$ 的圆的两条切线。$AQ = AS$....….(ii)将 (i) 和 (ii) 相加，得到，$AP + AQ = AR + AS$$PQ = RS$证毕。
已知：一个圆的外切四边形的三个连续边的长度分别为 \( 4 \mathrm{~cm} \)、\( 5 \mathrm{~cm} \) 和 \( 7 \mathrm{~cm} \)。求解：我们需要确定第四边的长度。解：在四边形 $ABCD$ 中，设 $BC = 4\ cm, CD = 5\ cm$ 和 $DA = 7\ cm$我们知道，如果一个四边形是圆的外切四边形，那么$AB + CD = AD + BC$$AB + 5 = 4 + 7$$AB + 5 = 11$$AB = 11 - 5 = 6$$AB = 6\ cm$第四边的长度为 6 cm。
已知：从圆外一点 \( P \) 引圆心为 \( O \) 的圆的两条切线 \( P A=P B \)。\( \angle P A B=50^{\circ} \)。求解：我们需要求 \( \angle A O B \) 的度数。解：$PA = PB$ （从圆外一点引圆的两条切线相等）$\angle PBA = \angle PAB = 50^o$ （对等边对应的角相等）在 $\triangle APB$ 中，$\angle PBA + \angle PAB + \angle APB =180^o$$\angle APB = 180^o - 50^o - 50^o = 80^o$在圆内接四边形 $OAPB$ 中，$\angle AOB + \angle APB = 180^o$ （圆内接四边形的对角互补… 阅读更多
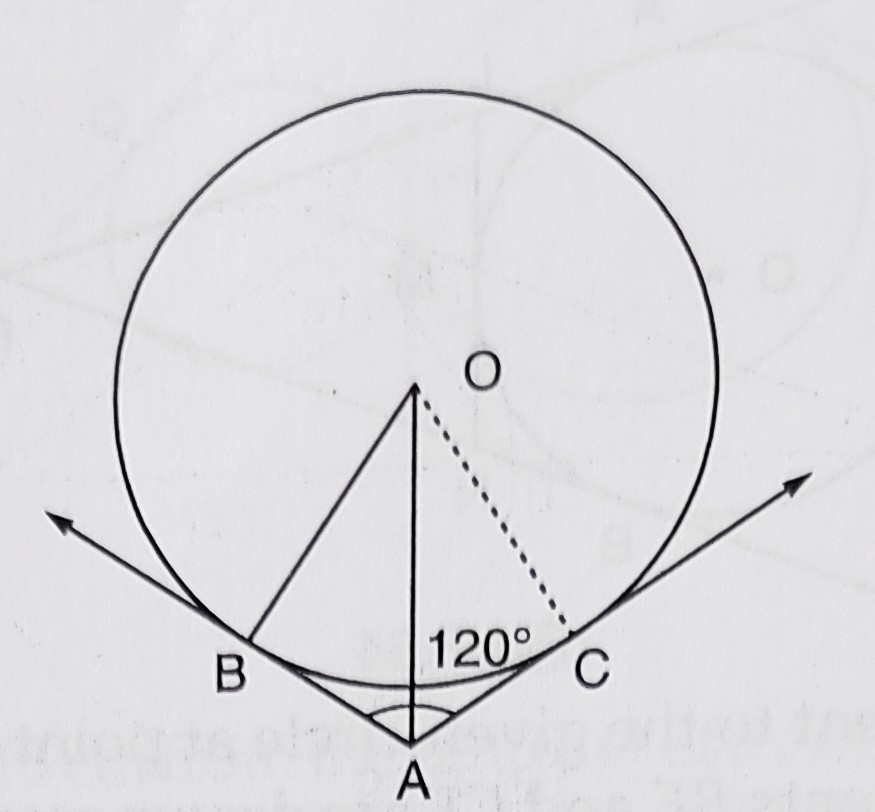
"\已知：如图所示，圆心为 \( O \) 的圆的两条切线 \( A B \) 和 \( A C \) 相交，且 \( \angle B A C=120^{\circ} . \)求解：我们需要证明 \( O A=2 A B \)。解：在 $\triangle OAB$ 和 $\triangle OAC$ 中，$\angle OBA = \angle OCA - 90^o$ ($OB$ 和 $OC$ 是半径)$OA = OA$ （公共边）$OB = OC$ （圆的半径）$\triangle OAB\ \sim\ \triangle OAC$$\angle OAB = \angle OAC = 60^o$在直角三角形 $OAB$ 中，$\cos 60^{\circ}=\frac{AB}{OA}$$\Rightarrow \frac{1}{2}=\frac{AB}{OA}$$\Rightarrow OA=2AB$证毕。
已知：\( d_{1}, d_{2}\left(d_{2}>d_{1}\right) \) 是两个同心圆的直径，\( c \) 是一个圆的弦长，该弦与另一个圆相切。要求：我们必须证明 \( d_{2}^{2}=c^{2}+d_{1}^{2} \)。解：设 $AB$ 是一个圆的弦，该弦与另一个圆在 $C$ 点相切。这意味着，$\triangle OCB$ 是一个直角三角形。根据勾股定理，$OC^2+CB^2=OB^2$$(\frac{1}{2} d_{1})^{2}+(\frac{1}{2} c)^{2}=(\frac{1}{2} d_{2})^{2}$ ($C$ 平分 $AB$) 因此，$d_{2}^{2}=c^{2}+d_{1}^{2}$证毕。