数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会研究
时尚研究
法律研究一座塔矗立在水平地面上，当太阳高度角为 30° 时，其影子比太阳高度角为 60° 时长 40 米。求塔的高度。
已知：一座塔矗立在水平地面上，当太阳高度角为 30° 时，其影子比太阳高度角为 60° 时长 40 米。
求解：求塔的高度。
解题步骤
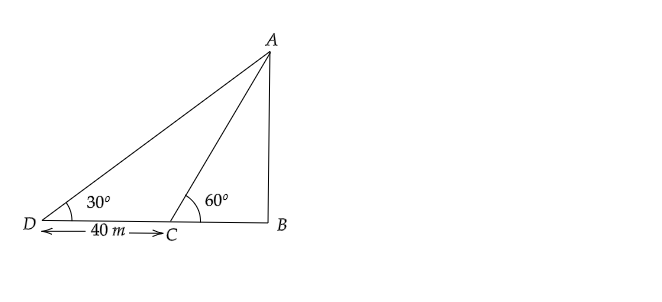
当太阳高度角为塔顶到影子顶端的仰角时。
设 AB 为 h 米，BC 为 x 米。
根据题意，DB 比 BC 长 40 米。
所以，BD = (40+x) 米，并形成两个直角三角形 ABC 和 ABD。
在△ABC 中，
tan 60° = AB/BC
⇒ √3 = h/x
⇒ x = h/√3 …… (i)
在△ABD 中，
⇒ tan 30° = AB/BD
⇒ 1/√3 = h/(x+40)
⇒ x+40 = √3h
⇒ h/√3 + 40 = √3h [使用 (i)]
⇒ h + 40√3 = 3h
⇒ 2h = 40√3
⇒ h = 40√3/2
⇒ h = 20√3
因此，塔的高度为 20√3 米。
更新于： 2022年10月10日
浏览量：135
广告