已知:入射光线与水平面夹角 = 10⁰求解:角 θ。解:根据反射定律,我们知道入射角 (i) 等于反射角 (r)。$(\angle i=\angle r)$这里,$Angle\ AOC(\angle i)=Angle\ BOC(\angle r)$因此, $( 90-\alpha ) +10=\alpha $ $[ \because \angle i=( 90-\alpha ) ,\ \angle AOD=10, \ and\ \angle r=\alpha ]$$90+10=\alpha+\alpha $ $2\alpha=100$ $\alpha=\frac {100}{2}$ $\alpha=50$ 现在, $\alpha+\beta=90$ $[ \because \angle COM=90]$将 α 的值代入上式,得到-$50+\beta=90$ $\beta=90-50$ $\beta=40$ 在 $\angle MOE$ 中 $\angle MOE+\angle ... 阅读更多
生产丝绸的步骤可以按以下正确的顺序排列:(e)雌蚕蛾产卵。(a)将蚕卵加热到合适的温度,使幼虫从卵中孵化出来。(d)将幼虫/毛虫或蚕放在干净的托盘中,并配上新鲜切碎的桑叶。(c)25 到 30 天后,毛虫停止进食并开始吐丝结茧。 (f)将茧放在阳光下或在水中煮沸。(b)从茧中取出纤维。家蚕的生命周期: ... 阅读更多
已知:四边形 $LION$,其中 $LI=6.5\ cm, \ IO=7.2\ cm, \ \angle I=90^o, \ \angle O = 60^o$ 和 $\angle N=105^o$。要求:作图:四边形 $LION$。解: 如给定,在四边形 $LION$ 中:$LI=6.5\ cm, \ IO=7.2\ cm, \ \angle I=90^o, \ \angle O = 60^o$ 和 $\angle N=105^o$$\Rightarrow \angle L +\angle I +\angle O+\angle N=360^o$$\Rightarrow \angle L+90^o+60^o+105^o=360^o$$\Rightarrow \angle L+255^o=360^o$$\Rightarrow \angle L=360^o-255^o$$\Rightarrow \angle L=105^o$1. 作图 $LI=6.5\ cm$。2. 在点 $L$ 处作角 $\angle XLI=105^o$。3. 在点 $I$ 处作角 $\angle I=90^o$。4. 以点 $I$ 为圆心,半径为 $7.2\ cm$ 作弧,该弧与直线相交于 $O$。 5. ... 阅读更多
已知:一栋房子的下窗户距离地面 \( 2 \mathrm{~m} \),上窗户在下方窗户垂直向上 \( 4 \mathrm{~m} \) 处。在某一时刻,从这两个窗户观察到一个气球的仰角分别为 \( 60^{\circ} \) 和 \( 30^{\circ} \)。要求:我们必须找到气球距离地面的高度。解:设气球距离地面的高度为 $H\ m$。从图中,$AB = ED =2\ m$$BC = EF = 4\ m$$GF = DG – (FE + ED)$$= H ... 阅读更多
已知:从一座高 \( h \) 米的塔顶,观察到两个物体在塔底同一直线上,它们的俯角分别为 \( \alpha \) 和 \(\beta(\beta>\alpha) \)。要求:我们必须找到这两个物体的距离。解:设这两个物体的距离为 $x\ m$,$DA= y\ m$,塔的高度为 $AB = h\ m$。从图中,$\angle XBC=\angle BCA = \alpha$ (内错角相等)$\angle XBD = \angle BDA = \beta$ ... 阅读更多
已知:从灯塔顶端,观察到两艘船在其相对的两侧,俯角分别为 \( \alpha \) 和 \( \beta \)。灯塔的高度为 \( h \) 米,并且连接这两艘船的直线经过灯塔的底部。要求:我们必须证明这两艘船之间的距离为 \( \frac{h(\tan \alpha+\tan \beta)}{\tan \alpha \tan \beta} \) 米。解:设 $AB$ 为灯塔,$C$ 和 $D$ 为两艘船,它们与 $B$ 的仰角分别为 $\alpha$ 和 $\beta$ ... 阅读更多
**已知:**一名木匠为电工制作凳子,凳子顶部为边长为\( 0.5 \mathrm{~m} \)的正方形,距地面高度为\( 1.5 \mathrm{~m} \)。此外,每条凳腿与地面成\( 60^{\circ} \)角。**求解:**我们需要求出每条凳腿的长度,以及需要放置在等距位置的两级台阶的长度。**解答:**设$AC$为凳子的凳腿,其顶部为边长为$AB$的正方形。凳子高度$AS = 1.5\ m$,凳腿与地面的倾斜角为... 阅读更多
**已知:**一个男孩站在地面上,放风筝,风筝线长\( 100 \mathrm{~m} \),仰角为\( 30^{\circ} \)。另一个男孩站在一栋\( 10 \mathrm{~m} \)高的建筑物屋顶上,也放风筝,仰角为\( 45^{\circ} \)。两个男孩分别站在两个风筝的对侧。**求解:**我们需要求出第二个男孩需要放多长的风筝线才能使两个风筝相遇。**解答:**设$F$为风筝,$A$和$C$为放风筝的两个男孩。男孩$C$站在... 阅读更多
**已知:**一位身高\( 1.5 \mathrm{~m} \)的观察者距离一栋高\( 30 \mathrm{~m} \)的塔\( 28.5 \mathrm{~m} \)。**求解:**我们需要确定塔顶到他眼睛的仰角。**解答:**设$AB$为塔,$CD$为观察者,他距离塔\( 28.5\ m\)。从图中可以看出,$AB = 30\ m, CD=1.5\ m, AC=28.5\ m$这意味着,$AE=CD=1.5\ m, DE=AC=28.5\ m$ 以及 $BE=30-1.5=28.5\ m$设\( \theta \)为塔顶到观察者眼睛的仰角。在$\Delta \mathrm{BDE}$中,$\tan \theta=\frac{\text { ... 阅读更多
**已知:**一把梯子与水平面成\( \alpha \)角靠在墙上。它的底部被拉离墙壁一段距离$a$,使得梯子沿墙壁下滑一段距离$b$ ,与水平面成\( \beta \)角。**求解:**我们需要证明\[\frac{a}{b}=\frac{\cos \alpha-\cos \beta}{\sin \beta-\sin \alpha}\]。**解答:**从图中可以看出,$AB$和$CD$是同一把梯子。这意味着$AB = CD$$\cos \alpha=\frac{\text { 底边 }}{\text { 斜边 }}$$=\frac{\mathrm{AE}}{\mathrm{AB}}$类似地,$\cos \beta=\frac{\mathrm{CE}}{\mathrm{CD}}$$=\frac{a+\mathrm{AE}}{\mathrm{AB}}$$\sin \alpha=\frac{\text { 高边 }}{\text { 斜边 }}$$=\frac{\mathrm{BE}}{\mathrm{AB}}$$=\frac{b+\mathrm{DE}}{\mathrm{AB}}$$\sin \beta=\frac{\mathrm{DE}}{\mathrm{CD}}$$=\frac{\mathrm{DE}}{\mathrm{AB}}$让我们考虑右边,$\frac{\cos \alpha-\cos \beta}{\sin \beta-\sin \alpha}=\frac{\frac{\mathrm{AE}}{\mathrm{AB}}-\frac{a+\mathrm{AE}}{\mathrm{AB}}}{\frac{\mathrm{DE}}{\mathrm{AB}}-\frac{b+\mathrm{DE}}{\mathrm{AB}}}$$=\frac{\mathrm{AE}-a-\mathrm{AE}}{\mathrm{DE}-b-\mathrm{DE}}$$=\frac{-a}{-b}$$=\frac{a}{b}$$= 左边$因此得证。 阅读更多

 数据结构
数据结构 网络
网络 关系型数据库管理系统
关系型数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP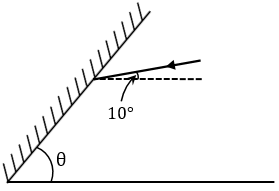 "\
"\