已知:由点 A(a, 2a), B(-2, 6) 和 C(3, 1) 形成的三角形 ABC 的面积为 10 平方单位。求解:我们需要找到 a 的值。解:我们知道,顶点为 (x1,y1), (x2,y2), (x3,y3) 的三角形的面积由以下公式给出:三角形面积 = 1/2[x1(y2-y3) + x2(y3-y1) + x3(y1-y2)]因此,三角形 ABC 的面积 = 1/2[a(6-1) - 2(1-2a) + 3(2a-6)]10 = 1/2[5a - 2 + 4a + 6a - 18]10(2) = (15a - 20)20 = 5(3a - 4)3a - 4 = 43a = 4 + 43a = 8a = 8/3a 的值为 8/3。
已知:给定点为 (a, a^2), (b, b^2), (0, 0)。a ≠ b ≠ 0求解:我们需要证明给定点永远不共线。解:设 A(a, a^2), B(b, b^2) 和 C(0, 0) 为三角形 ABC 的顶点。我们知道,如果点 A、B 和 C 共线,则三角形 ABC 的面积为零。顶点为 (x1, y1), (x2, y2), (x3, y3) 的三角形的面积由以下公式给出:三角形面积 = 1/2[x1(y2-y3) + x2(y3-y1) + x3(y1-y2)]因此,三角形 ABC 的面积 = 1/2[a(b^2-0) + b(0-a^2) + 0(a^2-b^2)] = 1/2[ab^2 - a^2b + 0] = 1/2[ab(b-a)] ≠ 0 (因为 a ≠ b ≠ 0)这里,三角形 ABC 的面积不为…阅读更多
已知:表达式:3x+8=14。求解:求解表达式:3x+8=14解:给定表达式:3x+8=14⇒ 3x+8=14⇒ 3x=14-8⇒ 3x=6⇒ x=6/3⇒ x=2因此,x=2。
已知:点 (a, 1), (1, -1) 和 (11, 4) 共线。求解:我们需要找到 a 的值。解:设 A(a, 1), B(1, -1) 和 C(11, 4) 为三角形 ABC 的顶点。我们知道,如果点 A、B 和 C 共线,则三角形 ABC 的面积为零。顶点为 (x1, y1), (x2, y2), (x3, y3) 的三角形的面积由以下公式给出:三角形面积 = 1/2[x1(y2-y3) + x2(y3-y1) + x3(y1-y2)]因此,三角形 ABC 的面积 = 1/2[a(-1-4) + 1(4-1) + 11(1+1)]0 = 1/2[a(-5) + 1(3) + 11(2)]0(2) = (-5a + 3 + 22)0 = -5a + 255a = 25a = 25/5a = 5a 的值为 5。 阅读更多
已知:给定点为 (a, b), (a1, b1) 和 (a – a1, b – b1)。求解:我们需要证明如果 ab1 = a1b,则点 (a, b), (a1, b1) 和 (a – a1, b – b1) 共线。解:设 A(a, b), B(a1, b1) 和 C(a-a1, b-b1) 为三角形 ABC 的顶点。我们知道,如果点 A、B 和 C 共线,则三角形 ABC 的面积为零。顶点为 (x1, y1), (x2, y2), (x3, y3) 的三角形的面积由以下公式给出:三角形面积 = 1/2[x1(y2-y3) + x2(y3-y1) + x3(y1-y2)]因此,三角形 ABC 的面积 = 1/2[a(b1-b+b1) + a1(b-b1-b) + (a-a1)(b-b1)] = 1/2[a(2b1-b) + a1(-b1) + (a-a1)(b-b1)] = 1/2[2ab1 - ab - ab1 + ab - ab1 - a1b + a1b1] = 1/2[ab1 - a1b] = 1/2[ab1 - ab1…阅读更多
已知:三角形的顶点为 (1, -3), (4, p) 和 (-9, 7),其面积为 15 平方单位。求解:我们需要找到 p 的值。解:设 A(1, -3), B(4, p) 和 C(-9, 7) 为三角形 ABC 的顶点。我们知道,顶点为 (x1, y1), (x2, y2), (x3, y3) 的三角形的面积由以下公式给出:三角形面积 = 1/2[x1(y2-y3) + x2(y3-y1) + x3(y1-y2)]因此,三角形 ABC 的面积 = 1/2[1(p-7) + 4(7+3) + (-9)(-3-p)]15 = 1/2[p - 7 + 4(10) + 27 + 9p]15(2) = (10p + 20 + 40)30 = 10p + 6010p = -60 + 30p = -30/10p = -3p 的值为 -3。 阅读更多
已知:三角形 ABC 的面积为 6 平方单位,其中 A(k+1, 1), B(4, -3) 和 C(7, -k)。求解:我们需要找到 k 的值。解:我们知道,顶点为 (x1, y1), (x2, y2), (x3, y3) 的三角形的面积由以下公式给出:三角形面积 = 1/2[x1(y2-y3) + x2(y3-y1) + x3(y1-y2)]因此,三角形 ABC 的面积 = 1/2[(k+1)(-3+k) + 4(-k-1) + 7(1+3)]6 = 1/2[-3k + k^2 - 3 + k - 4k - 4 + 7(4)]6(2) = (k^2 - 6k + 28 - 7)12 = k^2 - 6k + 21k^2 - 6k + 21 - 12 = 0k^2 - 6k + 9 = 0k^2 - 3k - 3k + 9 = 0k(k-3) - 3(k-3) = 0(k-3)(k-3) = 0(k-3)^2 = 0⇒ k-3 = 0k = 3k 的值为 3。 阅读更多
已知:(x, y) 在连接两点 (1, -3) 和 (-4, 2) 的直线上。求解:我们需要证明 x + y + 2 = 0。解:我们知道,如果点 A、B 和 C 共线,则三角形 ABC 的面积为零。设 A(1, -3), B(x, y) 和 C(-4, 2) 为三角形 ABC 的顶点。顶点为 (x1, y1), (x2, y2), (x3, y3) 的三角形的面积由以下公式给出:三角形面积 = 1/2[x1(y2-y3) + x2(y3-y1) + x3(y1-y2)]因此,三角形 ABC 的面积 = 1/2[1(y-2) + x(2+3) + (-4)(-3-y)]0 = 1/2[y - 2 + x(5) - (-4)(3+y)]0(2) = (y - 2 + 5x + 12 + 4y)0 = 5x + 5y + 105(x + y + 2) = 0x + y + 2 = 0证毕。阅读更多
已知:点 (k, 3), (6, -2) 和 (-3, 4) 共线。求解:我们需要找到 k 的值。解:设 A(k, 3), B(6, -2) 和 C(-3, 4) 为三角形 ABC 的顶点。我们知道,如果点 A、B 和 C 共线,则三角形 ABC 的面积为零。顶点为 (x1, y1), (x2, y2), (x3, y3) 的三角形的面积由以下公式给出:三角形面积 = 1/2[x1(y2-y3) + x2(y3-y1) + x3(y1-y2)]因此,三角形 ABC 的面积 = 1/2[k(-2-4) + 6(4-3) + (-3)(3+2)]0 = 1/2[k(-6) + 6(1) + (-3)(5)]0(2) = (-6k + 6 - 15)0 = -6k - 96k = -9k = -9/6k = -3/2k 的值为 -3/2。 阅读更多
**已知:**点 A(7, -2)、B(5, 1) 和 C(3, 2k) 共线。**求:**求 k 的值。**解:**设 A(7, -2)、B(5, 1) 和 C(3, 2k) 是△ABC 的顶点。我们知道,如果点 A、B 和 C 共线,则△ABC 的面积为零。顶点为 (x₁, y₁)、(x₂, y₂)、(x₃, y₃) 的三角形的面积由下式给出:三角形面积 = 1/2[x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)]因此,三角形 ABC 的面积 = 1/2[7(1-2k) + 5(2k+2) + 3(-2-1)]0 = 1/2[7 - 14k + 10k + 10 + 3(-3)]0(2) = (-4k + 17 - 9)0 = -4k + 84k = 8k = 8/4k = 2k 的值为 2。 阅读更多

 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
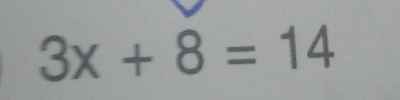 "\
"\