已知:多项式 $x^2+px+q$ 的零点是 $2x^2-5x-3$ 的零点的两倍。求解:求 $p$ 和 $q$ 的值。解:设 $\alpha$ 和 $\beta$ 是 $2x^2-5x-3$ 的零点。因此,零点之和 $\alpha+\beta=-\frac{b}{a}=-\frac{-5}{2}=\frac{5}{2}\ ......\ ( i)$ 零点之积 $\alpha\beta=\frac{c}{a}=\frac{-3}{2}\ ......\ ( ii)$。对于多项式 $x^2+px+q$:零点将是 $2\alpha$ 和 $2\beta$ 零点之和 $2\alpha+2\beta=-\frac{p}{1}=-p$ $\Rightarrow 2( \alpha+\beta)=-p$ $\Rightarrow 2 \times \frac{5}{2}=-p$ [由 $( i)\ \alpha+\beta=\frac{5}{2}$] $\Rightarrow p=-5$ 零点之积 $2\alpha.2\beta=\frac{q}{1}$ $\Rightarrow 4\alpha\beta=q$ $\Rightarrow 4\times( -\frac{3}{2})=q$ [由 $( ii)\ \alpha\beta=\frac{-3}{2}$] $\Rightarrow q=-6$ 因此,$p=-5$ 和 $q=-6$。阅读更多
已知:二次多项式的零点为 $\frac{3+\sqrt{5}}{5}$ 和 $\frac{3-\sqrt{5}}{5}$。求解:写出具有给定零点的多项式。解:如给定,多项式的零点为 $\frac{3+\sqrt{5}}{5}$ 和 $\frac{3-\sqrt{5}}{5}$。根之和 $=\alpha+\beta=\frac{3+\sqrt{5}}{5}+\frac{3-\sqrt{5}}{5}$ $=\frac{3+\sqrt{5}+3-\sqrt{5}}{5}$ $=\frac{6}{5}$ 零点之积 $\alpha\beta=( \frac{3+\sqrt{5}}{5})( \frac{3-\sqrt{5}}{5})$ $\Rightarrow \alpha\beta=\frac{( 3+\sqrt{5})( 3-\sqrt{5})}{5\times5}$ $\Rightarrow \alpha\beta=\frac{3^2-( \sqrt{5})^2}{25}$ $\Rightarrow \alpha\beta=\frac{9-5}{25}$ $\Rightarrow \alpha\beta=\frac{4}{25}$ 因此,多项式:$x^2-( \alpha+\beta)x+( \alpha\beta)=0$ $\Rightarrow x^2-\frac{6}{5}x+\frac{4}{25}=0$ $\Rightarrow 25x^2-30x+4=0$ 因此,多项式为 $25x^2-30x+4=0$。阅读更多
已知:二次多项式的零点为 $-2$ 和 $-5$。求解:求多项式。解:如给定,二次多项式的零点为 $-2$ 和 $-5$。因此,零点之和 $\alpha+\beta=-2+(-5)=-7$ 零点之积 $\alpha\beta=(-2)\times(-5)=10$ 因此,多项式为:$x^2-(\alpha+\beta)x+\alpha\beta=0$ $\Rightarrow x^2-(-7)x+10=0$ $\Rightarrow x^2+7x+10=0$ 因此,多项式为 $x^2+7x+10=0$。
已知:多项式 $4x^2+4x-3$。求解:证明 $\frac{1}{2}$ 和 $-\frac{3}{2}$ 是多项式 $4x^2+4x-3$ 的零点。解:设 $p(x)=4x^2+4x-3$ 如果 $\frac{1}{2}$ 和 $-\frac{3}{2}$ 是多项式 $4x^2+4x-3$ 的零点,那么它们将满足该多项式。$\Rightarrow p(\frac{1}{2})=4(\frac{1}{2})^2+4(\frac{1}{2})-3$ $\Rightarrow p(\frac{1}{2})=4(\frac{1}{4})+2-3$ $\Rightarrow p(\frac{1}{2})=1+2-3$ $\Rightarrow p(\frac{1}{2})=0$ 因此,$\frac{1}{2}$ 是多项式 $4x^2+4x-3$ 的零点。现在,$p(-\frac{3}{2})=4(-\frac{3}{2})^2+4(-\frac{3}{2})-3$ $\Rightarrow p(-\frac{3}{2})=4(\frac{9}{4})+2(-3)-3$ $\Rightarrow p(-\frac{3}{2})=9-6-3$ $\Rightarrow p(-\frac{3}{2})=0$ 因此,已证明 $\frac{1}{2}$ 和 $-\frac{3}{2}$ 是多项式 $4x^2+4x-3$ 的零点。阅读更多
已知:一个二次多项式,其零点的和与积分别为 $-8$ 和 $12$。求解:求其零点。解:设 $\alpha$ 和 $\beta$ 是二次多项式的零点。如给定,零点之和 $=\alpha+\beta=-8$ 零点之积 $=\alpha\beta=12$ 二次多项式:$x^2-(\alpha+\beta)x+\alpha\beta=0$ $\Rightarrow x^2-(-8)x+12=0$ $\Rightarrow x^2+8x+12=0$ 因此,二次多项式为 $x^2+8x+12=0$。
已知:一个二次多项式的零点之和与积分别为 $0$ 和 $-\frac{3}{5}$。求解:写出多项式,并求其零点。解:设 $\alpha$ 和 $\beta$ 是二次多项式的零点。如给定 $\alpha+\beta=0$ 和 $\alpha\beta=-\frac{3}{5}$ 多项式为:$x^2-(\alpha+\beta)x+\alpha\beta=0$ $\Rightarrow x^2-(0)x+(-\frac{3}{5})=0$ $\Rightarrow x^2-\frac{3}{5}=0$ $\Rightarrow 5x^2-3=0$ $\Rightarrow x^2=\frac{3}{5}$ $\Rightarrow x=\pm\sqrt{\frac{3}{5}}$ 因此,多项式为 $5x^2-3=0$,零点为 $x=\sqrt{\frac{3}{5}},\ -\sqrt{\frac{3}{5}}$。
已知:二次多项式 $6x^2-3-7x$。求解:求二次多项式 $6x^2-3-7x$ 的零点,并验证零点与多项式系数之间的关系。解:给定多项式为 $6x^2-3-7x$。$=6x^2-7x-3$ $=6x^2-9x+2x-3$ $=3x(2x-3)+1(2x-3)$ $=(2x-3)(3x+1)$ 如果 $(2x-3)=0$ $\Rightarrow x=\frac{3}{2}$ 如果 $(3x+1)=0$ $\Rightarrow x=-\frac{1}{3}$ 因此,$x=\frac{3}{2}, -\frac{1}{3}$ 根之和 $=\frac{3}{2}+(-\frac{1}{3})=\frac{9-2}{6}=\frac{7}{6}=-\frac{-b}{a}$ [已验证] 根之积 $=\frac{3}{2}\times(-\frac{1}{3})=-\frac{3}{6}=-\frac{1}{2}=\frac{c}{a}$ [已验证]阅读更多
已知:数字:$\frac{17}{40}$ 和 $0.519$。解:给定数字:$\frac{17}{40}$ 和 $0.519$。$\frac{17}{40}=0.425$ $\Rightarrow 0.425
已知:$( i). \ y+3=10$ $( ii).\ 6x=12$。求解:解给定方程。解:$( i). \ y+3=10$ $\Rightarrow y=10-3$ $\Rightarrow y=7$ 因此,$y=7$。$( ii).\ 6x=12$ $\Rightarrow x=\frac{12}{6}$ $\Rightarrow x=2$ 因此,$x=2$。
已知:方程 $n-2=7$。求解:解给定方程。解:如给定方程 $n-2=7$ $\Rightarrow n=7+2$ $\Rightarrow n=9$ 因此,$n=9$

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
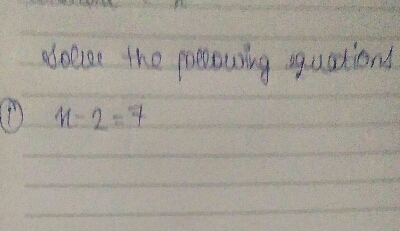 "\
"\