已知:方程:$\frac{4}{x} -3=\frac{5}{2x+3} ;\ x \ne 0,\ \frac{-3}{2}$ 求解:求解给定方程的 x。解答:给定方程为:$\frac{4}{x} -3=\frac{5}{2x+3} ;\ x \ne 0,\ \frac{-3}{2}$$\frac{4}{x} -3=\frac{5}{2x+3} ;\ x \ne 0,\ \frac{-3}{2}$$\Rightarrow \frac{4-3x}{x} =\frac{5}{2x+3}$$\Rightarrow ( 4-3x)( 2x+3) =5x$$\Rightarrow 8x+12-6x^{2} -9x=5x$$\Rightarrow -6x^{2} -6x+12=0$$\Rightarrow -6\left( x^{2} +x-2\right) =0$$\Rightarrow x^{2} +x-2=0$$\Rightarrow x^{2} +2x-x-2=0$$x( x+2) -1( x+2) =0$$( x+2)( x-1) =0$如果 $x+2=0$$\Rightarrow x=-2$如果 $x-1=0$$\Rightarrow x=1$因此 $x=-2,\ 1$
已知:等差数列的第七项是 $\frac{1}{9}$,第九项是 $\frac{1}{7}$。求解:求该等差数列的第 63 项。解答:设 a 为首项,d 为公差。已知等差数列的第 n 项,$a_{n} =a+( n-1) d$则该等差数列的第七项 $a_{7} =a+( 7-1) d$$\Rightarrow \frac{1}{9} =a+6d\ \ \ \ ...........( 1)$同样,该等差数列的第九项$a_{9} =a+( 9-1) d$$\frac{1}{7} =a+8d\ \ \ \ \ \ \ \ \ .............( 2)$从 (1) 减去 (2)$a+8d-a-6d=\frac{1}{7} -\frac{1}{9}$$\Rightarrow 2d=\frac{2}{63}$$\Rightarrow d=\frac{1}{63}$,代入… 阅读更多
已知:$\frac{\frac{50}{3} \ -\ \frac{200}{9}}{5}$ 求解:我们需要计算 $\frac{\frac{50}{3} \ -\ \frac{200}{9}}{5}$ 的值。解答:$\frac{\frac{50}{3} \ -\ \frac{200}{9}}{5}$$ \begin{array}{l}3\ 和\ 9\ 的最小公倍数是\ 9,\ 所以\\\end{array}$= $\frac{\frac{50}{3} \ -\ \frac{200}{9}}{5} \ =\ \frac{\frac{50\ \times \ 3\ -\ 200}{9}}{5}$= $\frac{150\ -\ 200}{9\ \times \ 5}$= $\frac{-50}{45}$= $\frac{-10}{9}$
已知:拉希姆同时抛掷两枚硬币。求解:求至少得到一枚反面的概率。解答:拉希姆同时抛掷两枚硬币。该实验的样本空间是(HH, HT, TH, 和 TT)。总结果数 = 4 至少得到一枚反面的结果 = (HT, TH, TT) 至少得到一枚反面的结果数 = 3 抛掷两枚硬币至少得到一枚反面的概率 = $\frac{有利结果总数}{总结果数}$ = $\frac{3}{4}$ 因此,至少得到一枚反面的概率是 $\frac{3}{4}$。阅读更多
已知:正方形 OABC 内接于象限 OPBQ。OA = 20 厘米。求解:求阴影区域的面积。解答:如图所示,OABC 是正方形,OA=AB=BC=CA=20 厘米连接 OB。在三角形 OAB 中,$OB^{2} =OA^{2} +AB^{2}$$\Rightarrow \ OB^{2} =20^{2} +20^{2}$$\Rightarrow OB^{2} =400+400$$\Rightarrow OB=\sqrt{800}$$\Rightarrow OB=20\sqrt{2}$OB 是给定象限的半径 r。给定象限的面积,$A_{1} =\frac{\theta }{360^{o}} \times \pi r^{2}$$A_{1} =\frac{90^{o}}{360^{o} } \times 3.14\times \left( 20\sqrt{2}\right)^{2}$$\Rightarrow A_{1} =\frac{1}{4} \times 3.14\times 800$$\Rightarrow A_{1} =628cm^{2}$正方形的面积 $A_{2} =( 边长)^{2}$$\Rightarrow A_{2} =20\times 20$$\Rightarrow A_{2} =400cm^{2}$阴影区域的面积,A = 象限面积,$A_{1} -$正方形… 阅读更多
已知:从圆外一点到圆心 O 引两条切线 PQ 和 PR,使得 $\angle $QPR = 120^{o} 求解:证明 $2PQ=PO$。解答:让我们画一个以 P 为外点,PQ 和 PR 为两条切线的圆。我们知道,半径垂直于切点处的切线。$\angle OQP=90^{o} $我们也知道,从外一点引出的两条切线与连接该点和圆心的线段等角倾斜。$\angle QPO=60^{o}$现在,在三角形 QPO 中:$cos60^{o}=\frac{PQ}{PO}$$\Rightarrow \frac{1}{2} =\frac{PQ}{PO}$$\Rightarrow PO=2PQ$因此证明了 $PO=2PQ$。 阅读更多
已知:二次方程 $2x^{2} +ax-a^{2} =0$。求解:求解给定二次方程的 x。解答:给定二次方程 $2x^{2} +ax-a^{2} =0$,将给定二次方程与 $ax^{2} +bx+c=0$ 相比较,我们有 $a=2, b=a$ 和 $c=-a^{2}$我们知道对于二次方程 $x=\frac{-b\pm \sqrt{b^{2} -4ac}}{2a}$使用上述二次方程公式,$x=\frac{-a\pm \sqrt{a^{2} -4\times 2\times ( -a)^{2}}}{2\times 2}$$\Rightarrow x=\frac{-a\pm \sqrt{a^{2} +8a^{2}}}{4}$$\Rightarrow x=\frac{-a\pm \sqrt{9a^{2}}}{4}$$\Rightarrow x=\frac{-a\pm 3a}{4}$$\Rightarrow x=\frac{-a+3a}{4} \ or\ \frac{-a-3a}{4}$$\Rightarrow x=\frac{2a}{4} \ or\ \frac{-4a}{4}$$\Rightarrow x=\frac{a}{2}$ 或 $-a$因此,给定二次方程的解为 $x=\frac{a}{2}$ 或 $-a$。 阅读更多
已知:等差数列,首项和末项分别为 5 和 45。所有项的和 = 400。求解:求其公差。解答:设 a 为首项,d 为公差。假设给定的等差数列有 n 项。这里,根据已知条件,首项 a=5 末项 l=45 等差数列的和 $S_{n}=400$$n=?$根据已知条件,末项 $l=a_{n}=a+(n-1)d$$\Rightarrow 45=5+(n-1)d$$\Rightarrow ( n-1) d=40\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ .................( 1)$所有项的和 $S_{n} =\frac{n}{2}[ 2a+( n-1) d]$$\Rightarrow \frac{n}{2}[ 2\times 5+40] ... 阅读更多
已知:圆的两条平行切线和连接这两条切线的切点的线段。求证:该线段经过圆心。证明:设XBY和PCQ是圆的两条平行切线,圆心为O。连接OB和OC。由于XB平行于AO,我们知道邻补角之和为180°。因此,∠XBO + ∠AOB = 180°。∠XBO = 90°(圆的切线垂直于过切点的半径)。则90° + ∠AOB = 180°,所以∠AOB = 90°。同理……阅读更多
摄氏度和开尔文温标之间的关系是:K = C + 273.15 0摄氏度等于273.15开尔文。

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
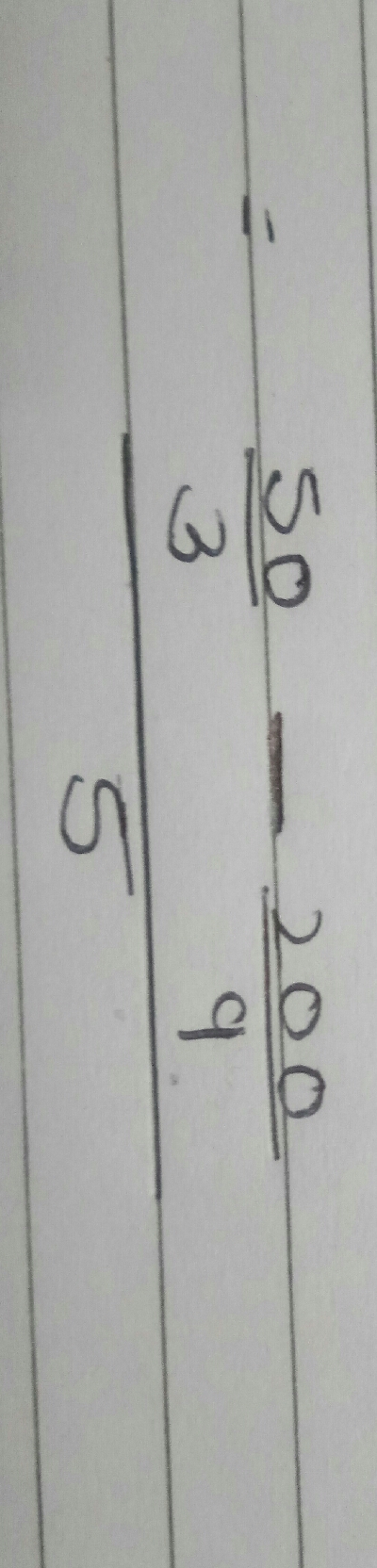 "\
"\ "\
"\