生成式AI模型 - 最大似然估计

上一页
下一页

最大似然估计 (MLE) 是一种统计方法，它提供了一种主要方法来估计概率分布的参数，该分布最能描述给定的数据集。MLE 假设指定的分布生成了数据。简单来说，MLE 是一种用于找出模型未知参数（例如一组数据点的平均值或分布）最可能值的方法。这就像我们猜测序列中缺失的数字，以便它符合我们已经知道的数字模式。

在生成式 AI 领域，尤其是在生成对抗网络 (GAN) 和变分自编码器 (VAE) 等生成模型中，MLE 具有广泛的应用。例如，在生成手写数字 (0-9) 的图像时，我们希望我们的模型生成的图像类似于我们数据集中（如 MNIST）的图像。我们可以通过最大化给定模型参数的情况下观察训练数据的可能性来实现这一点。

maximize Σ log P(x | θ)

我们稍后将在使用 Python 编程语言创建我们的第一个 GAN 模型时详细介绍这一点。阅读本章以了解最大似然估计的概念、其在生成建模中的重要作用、MLE 在生成建模中的应用及其 Python 实现。

理解最大似然估计 (MLE)

最大似然估计 (MLE) 是一种强大的统计方法，用于根据观察到的数据估计概率分布的参数。让我们借助其数学基础更详细地了解它：

MLE 的数学基础

MLE 的核心是似然函数：$\mathrm{L(\theta | x)}$。这里，$\mathrm{\theta}$ 表示分布的参数，x 表示观察到的数据。

似然函数量化了给定特定参数值的情况下观察数据的概率。从数学上讲，它表示为观察数据的联合概率密度函数 (PDF) 或概率质量函数 (PMF)。

$$\mathrm{L(\theta | x) \: = \: f(x | \theta)}$$

为了简化计算，我们通常使用对数似然函数 $\mathrm{l(\theta | x)}$，它是似然函数的自然对数：

$$\mathrm{l(\theta | x) \: = \: \log L(\theta | x)}$$

实际上，MLE 的目标是找到最大化似然函数 $\mathrm{L(\theta | x)}$ 或等效地最大化对数似然函数 $\mathrm{l(\theta | x)}$ 的参数值 $\mathrm{\hat{\theta}}$：

$$\mathrm{\hat{\theta} \: = \: argmax_{\theta} L(\theta | x)}$$

或者，

$$\mathrm{\hat{\theta} \: = \: argmax_{\theta} l(\theta | x)}$$

现在，为了获得最大似然估计 $\mathrm{\hat{\theta}}$，我们对对数似然函数 $\mathrm{l(\theta | x)}$ 关于参数 $\mathrm{\theta}$ 求导，并将导数设置为零：

$$\mathrm{\frac{\partial \: l(\theta | x)}{\partial \: \theta} \: = \: 0}$$

求解上述方程得到 MLE $\mathrm{\hat{\theta}}$。

生成建模中的 MLE

正如我们前面讨论的，生成建模涉及捕获数据的潜在分布并生成与原始训练数据相当的新数据。在训练生成模型时，MLE 通过估计潜在概率分布的参数发挥着至关重要的作用。

让我们看看如何在生成建模中应用 MLE：

模型选择

我们首先需要选择一个能够捕获潜在数据分布的概率模型。一些常见的模型包括高斯分布、混合模型、神经网络等。

似然函数

接下来，我们需要定义似然函数。此似然函数衡量观察到给定数据的概率。例如，对于给定的数据集 $\mathrm{D \: = \: \lbrace x_{1},x_{2},x_{3},\: \dots \: x_{n} \rbrace}$，似然函数 $\mathrm{L(\theta | D)}$ 取决于模型参数 $\mathrm{\theta}$，并且由观察每个数据点的概率的乘积给出：

$$\mathrm{L(\theta | D) \: = \: \prod_{i=1}^N p(x_{i} | \theta)}$$

最大化

现在我们需要根据模型参数 $\mathrm{\theta}$ 最大化似然函数。最大化包括找到使在模型下观察到的数据最有可能的 $\mathrm{\theta}$ 值。

参数估计

最后，当似然函数最大化时，所得参数值将用作生成模型参数的估计值。这些估计的参数定义了学习到的分布，然后可以使用它来生成与观察到的数据相当的新数据点。

MLE 在生成建模中的应用

MLE 在生成建模的各个领域都有广泛的应用。下面是一些重要的应用：

  • 高斯混合模型 (GMM) - MLE 用于估计 GMM 中高斯分量的参数。这些参数能够对具有多个模式的复杂数据分布进行建模。
  • 变分自编码器 (VAE) - 在 VAE 中，MLE 用于学习潜在变量分布的参数。它允许模型通过从此学习到的分布中采样来生成新的数据样本。
  • 生成对抗网络 (GAN) - GAN 不直接优化似然函数，但 MLE 用于 GAN 的训练以指导学习过程并提高样本质量。

使用 Python 实现最大似然估计

我们可以使用 Python 实现 MLE，并使用 Matplotlib 等库对其进行可视化。下面是一个简单的示例，用于执行 MLE 以根据给定的数据集估计高斯分布的参数：

示例

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# Sample dataset (you can replace this with your own data)
data = np.random.normal(loc=2, scale=1, size=2000)

# Maximum Likelihood Estimation for a Gaussian distribution
def maximum_likelihood_estimation(data):
   # Calculate the mean and standard deviation of the data
   mu = np.mean(data)
   sigma = np.std(data)
   return mu, sigma

# Perform Maximum Likelihood Estimation
estimated_mu, estimated_sigma = maximum_likelihood_estimation(data)

# Generate x values for plotting
x = np.linspace(min(data), max(data), 1000)

# Plot histogram of the data
plt.figure(figsize=(7.2, 5.5))
plt.hist(data, bins=30, density=True, alpha=0.6, color='blue', label='Data Histogram')

# Plot the true Gaussian distribution
plt.plot(x, norm.pdf(x, loc=2, scale=1), color='red', linestyle='--', label='True Gaussian Distribution')

# Plot the estimated Gaussian distribution using MLE
plt.plot(x, norm.pdf(x, loc=estimated_mu, scale=estimated_sigma), color='green', linestyle='-', label='Estimated Gaussian Distribution (MLE)')

plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.title('Maximum Likelihood Estimation for Gaussian Distribution')
plt.legend()
plt.grid(True)

plt.show()

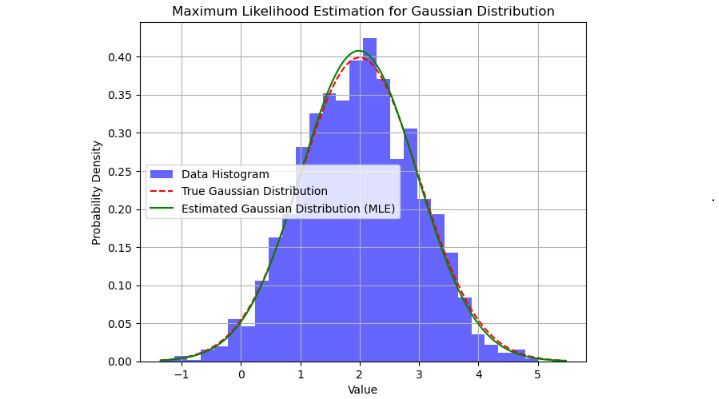
输出

上面的代码将生成一个图，显示数据的直方图、真实的高斯分布以及使用最大似然估计 (MLE) 获得的估计高斯分布。

Maximum Likelihood Estimation

结论

在本章中，我们强调了 MLE 在生成建模中的重要性。在生成建模中，MLE 作为学习数据分布和生成新样本的支柱。

模型选择、似然函数、最大化和参数估计是我们可以在生成建模中应用 MLE 的步骤。

打印页面
上一页
下一页
广告