生成式AI模型中概率密度函数的作用

上一页
下一页

概率分布可以是离散的或连续的。

  • 离散概率分布更适合于结果只能取离散或分类随机变量的场景。
  • 当结果在连续的值范围内取任何值时，连续概率分布更合适。

在生成建模的背景下，连续概率分布作为一种强大的工具，旨在在广泛的应用中创建逼真且多样化的数据样本。事实上，它们帮助生成模型更好地理解和模拟现实世界的数据。

连续概率分布背后的关键概念之一是概率密度函数（PDF），它描述了连续随机变量（如时间、重量或高度）在给定范围内取特定值的可能性。在本章中，我们将详细地解释概率密度函数。

理解概率密度函数（PDF）

对于离散变量，我们可以很容易地计算概率。但是，另一方面，对于连续变量，计算概率相当困难，因为概率取一系列无限的值。在统计学中，描述此类变量概率的函数称为概率密度函数（PDF）。

简单来说，概率密度函数是一个定义连续随机变量（例如X）与其概率之间关系的函数。我们可以使用该函数找到变量X的概率。

在数学上，连续随机变量X的PDF f(x)必须满足以下属性：

  • $\mathrm{f(x) \geq 0}$ 对于X范围内的所有x。
  • PDF曲线在X所有可能取值上的总面积等于1。这表示总概率空间。
  • X落在特定区间[a,b]内的概率由f(x)在该区间上的积分给出：$\mathrm{\int_{a}^{b} \: f(x) \: dx}$。

绘制PDF后，我们将得到如下图形：

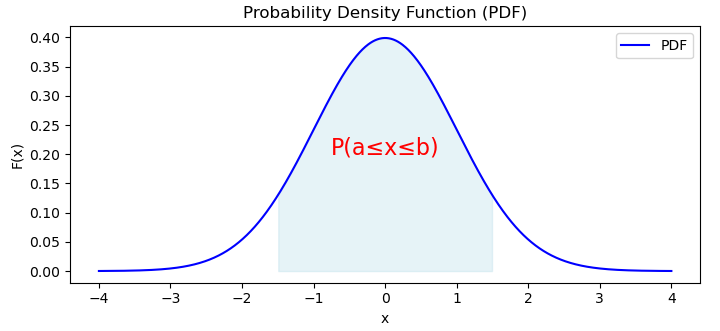
Probability Density Functions 1

概率分布函数是概率论中的一个基本概念，它为我们提供了概率分布的连续表示，使我们能够理解在连续域中不同结果发生的可能性。它广泛应用于机器学习、统计学和物理学等各个领域。

使用Python实现概率密度函数

在Python中，要找到给定数据集的概率密度函数（PDF），我们可以使用NumPy和Matplotlib等库。下面是一个计算和绘制数据集PDF的简单示例：

示例

# importing necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# Creating Sample dataset 
data = np.random.normal(loc=0, scale=1, size=1000)

# Fit a Gaussian distribution to the data
mu, std = norm.fit(data)

# Plot the histogram of the data
plt.figure(figsize=(7.2, 2.5))
plt.hist(data, bins=50, density=True, alpha=0.5, color='cyan')

# Plot the PDF of the fitted Gaussian distribution
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, mu, std)
plt.plot(x, p, 'g', linewidth=2)

plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.title('Probability Density Function (PDF)')
plt.grid(True)

plt.show()

在上面的代码中，我们首先使用NumPy的np.random.normal()函数生成一个随机数据集。

然后，我们使用SciPy的norm.fit()将高斯分布拟合到数据。此函数返回拟合的高斯分布的均值（mu）和标准差（std）。

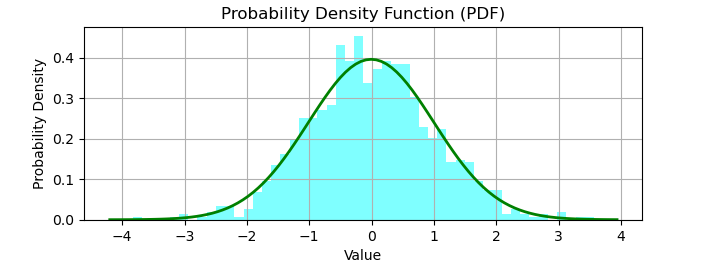
之后，我们使用Matplotlib的plt.hist()绘制数据的直方图。最后，我们在直方图上绘制平滑的钟形曲线（PDF）。

输出

运行此代码后，您将获得如下输出图形：

Probability Density Functions 2

概率密度函数在生成建模中的作用

在生成建模中，概率密度函数（PDF）发挥着几个关键作用，如下所示：

建模数据分布

建模数据分布是生成建模中的重要任务之一。众所周知，概率密度函数提供了潜在数据分布的数学表示。PDF帮助生成模型最佳地描述观察到的数据。

数据采样

一旦生成模型学习了PDF，它就可以用于从建模的数据分布中采样新的数据点。此采样过程帮助生成模型生成与原始数据非常相似的新数据样本。

似然估计

许多生成建模算法（如最大似然估计（MLE）和变分推断）都使用似然估计。PDF通过估计给定分布参数下观察到特定数据点的可能性来帮助生成模型。

生成对抗网络（GAN）

在GAN中，我们有一个称为生成器的网络。生成器通过捕获潜在数据分布来学习生成逼真的数据样本。它通常输出遵循连续分布的数据点，并且与此分布相关的概率密度函数指导学习过程。

变分自动编码器（VAE）

VAE学习一个低维潜在空间，该空间捕获数据的显著特征。概率密度函数用于对潜在变量的分布进行建模。它允许模型通过从该潜在空间中采样并将样本解码到原始数据空间来生成新的数据样本。

模型性能评估

概率密度函数也可用于评估生成模型的性能。一些指标（如对数似然或散度度量）量化了学习到的分布与真实数据分布的匹配程度。它为我们提供了对生成样本质量的见解。

结论

在本章中，我们详细解释了概率密度函数（PDF）、其在Python中的实现及其在生成建模中的多方面作用。

PDF是概率论中的一个基本概念，它为我们提供了概率分布的连续表示，帮助我们理解在连续域中不同结果发生的可能性。我们了解了PDF如何定义连续随机变量与其概率之间的关系。

我们还通过一个示例演示了如何使用Python实现概率密度函数。概率密度函数是生成建模中必不可少的工具，它能够表示、采样和评估数据分布，并作为各种生成建模算法的基础。

打印页面
上一页
下一页
广告