一个人在船上，划船远离一座高100米高的灯塔，用了2分钟时间将灯塔顶部的仰角从60°变为30°。求船的速度（米/分钟）。（使用√3=1.732）

已知

一个人在船上，划船远离一座高100米高的灯塔，用了2分钟时间将灯塔顶部的仰角从60°变为30°。

要求

我们必须求出船的速度。

解答

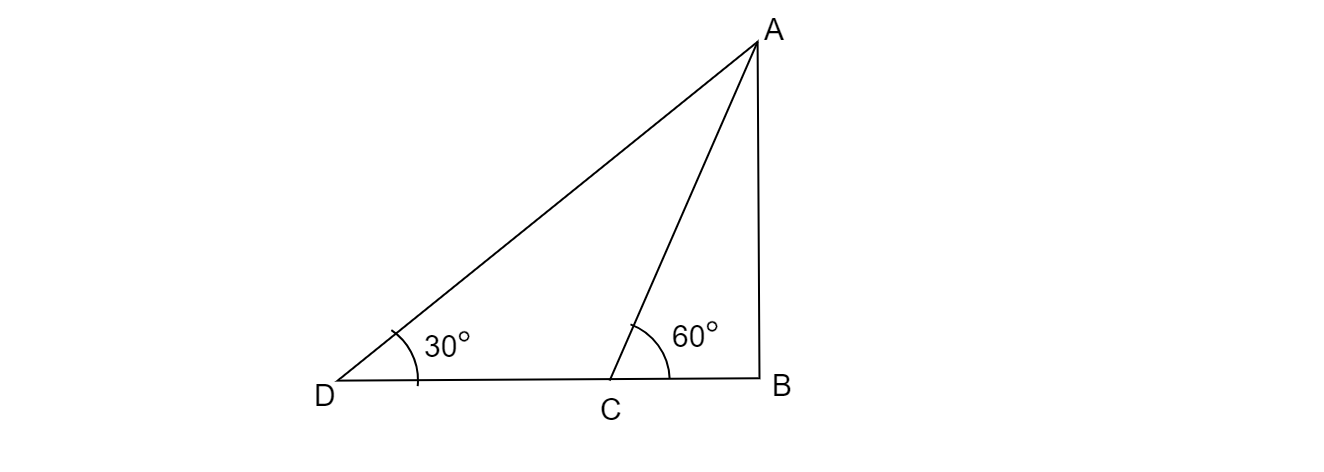
AB是一座高100米高的灯塔。

设船的速度为x米/分钟，CD为该人在2分钟内行进的距离。

距离=速度×时间

因此，

CD=x×2=2x

在△ABC中，

tan 60°=AB/BC

⇒ √3=100/BC

⇒ BC=100/√3

在△ABD中，

tan 30°=AB/BD

⇒ 1/√3=100/BD

⇒ BD=100√3

从图中，

CD=BD-BC

⇒ 2x=100√3-100/√3

⇒ 2x=(300-100)/√3

⇒ 2x=200/√3

⇒ x=(1/2)(200/√3)

⇒ x=100/√3

⇒ x=100/1.732≈57.80 米/分钟

因此，船的速度为57.80米/分钟。

更新于：2022年10月10日

浏览量：344

开启您的职业生涯

完成课程获得认证

开始学习
广告