数据结构
网络
关系数据库管理系统(RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究海上有两艘船位于灯塔的两侧，使得船和灯塔在同一条直线上。从灯塔顶端观察两艘船的俯角分别为 \( 60^{\circ} \) 和 \( 45^{\circ} \)。如果灯塔的高度为 \( 200 \mathrm{~m} \)，求两艘船之间的距离。（使用 \( \sqrt{3}=1.73 \)）
已知
一座高 $200\ m$ 的灯塔，从灯塔顶端观察到两艘船的俯角分别为 $60^{o} $ 和 $45^{o}$。
要求
求两艘船之间的距离。
解答
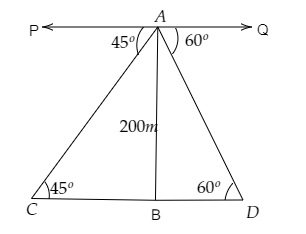
设两艘船分别为 $C$ 和 $D$，$AB$ 为灯塔，两船之间的距离为 $d$。
假设其中一艘船到灯塔的距离为 $x$ 米，则另一艘船到灯塔的距离为 $(d-x)\ m$。
在直角三角形 $\vartriangle ABC$ 中，我们有
$tan45^{o}=\frac{AB}{BC}$
$\Rightarrow 1=\frac{200}{x}$
$\Rightarrow x=200\ m$......(i)
在直角三角形 $\vartriangle ABD$ 中，
$tan60^{o}=\frac{AB}{d-x}$
$\Rightarrow \sqrt{3} =\frac{200}{d-200}$ [由 (i) 式]
$\Rightarrow \sqrt{3}( d-200) =200$
$d\sqrt{3} -200\sqrt{3} =200$
$\Rightarrow d\sqrt{3} =200+200\sqrt{3}$
$\Rightarrow d=200\left(\frac{1+\sqrt{3}}{\sqrt{3}}\right)$
$\Rightarrow d=200\times 1.58$
$\Rightarrow d=316$
因此，两艘船之间的距离约为 $316\ m$。
更新于: 2022年10月10日
浏览量：57
广告