一个高3厘米的物体放置在一个凹面镜前8厘米处，该凹面镜产生一个高4.5厘米的虚像：(i) 镜子的焦距是多少？(ii) 像的位置在哪里？(iii) 画一个光线图来显示像的形成。

物体到镜面的距离 $u$ = $-$8 cm

物体的高度，$h_{1}$ = 3 cm

像的高度 $h_{2}$ = 4.5 cm

求解：镜子的焦距 $f$，以及像到镜面的距离 $v$。

解答

根据放大倍数公式，我们知道：

$m=\frac{{h}_{2}}{{h}_{1}}=-\frac{v}{u}$

将已知值代入放大倍数公式，我们得到：

$\frac{4.5}{3}=-\frac{v}{(-8)}$

$\frac{4.5}{3}=\frac{v}{8}$

$3v={4.5}\times {8}$

$v=\frac{{4.5}\times {8}}{3}$

$v={1.5}\times {8}$

$v=+12cm$

因此，像的距离 $v$ 为12 cm，正号表示像形成在镜面后面（右侧）。

现在，根据镜面公式，我们知道：

$\frac{1}{f}=\frac{1}{v}+\frac{1}{u}$

将已知值代入镜面公式，我们得到：

$\frac{1}{f}=\frac{1}{12}+\frac{1}{(-8)}$

$\frac{1}{f}=\frac{1}{12}-\frac{1}{8}$

$\frac{1}{f}=\frac{2-3}{24}$

$\frac{1}{f}=\frac{-1}{24}$

$f=-24cm$

因此，凹面镜的焦距 $f$ 为 24 cm，负号表示焦点在凹面镜前面（左侧）。

(ii) $v=12$（上面计算得出）。

因此，像的位置在镜面后面 12 cm 处。

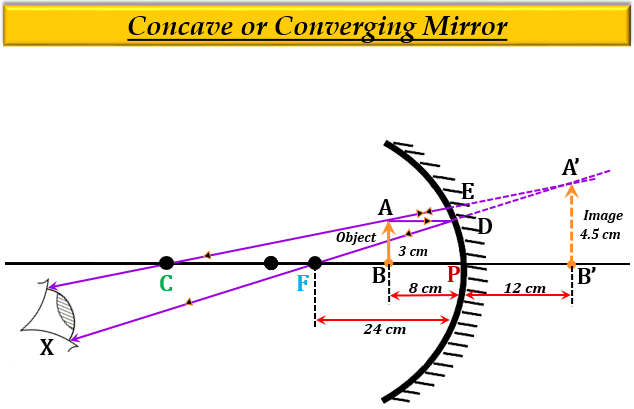
(iii) 显示像形成的光线图。

教程点

更新于： 2022年10月10日

3K+ 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习