如果∠B和∠Q是锐角，且满足$Sin B = Sin Q$，则证明$∠ B = ∠ Q$。

已知

$Sin B = Sin Q$

要求

我们需要证明$∠ B = ∠ Q$。

解答

考虑两个直角三角形ABC和PQR，其中$sin B = sin Q$。

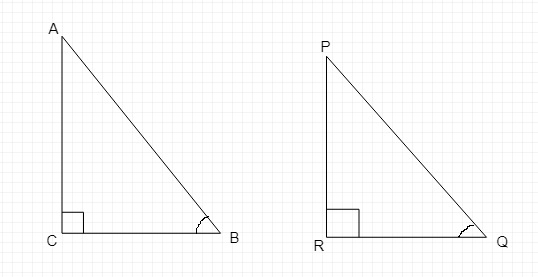
从图中，

$Sin B = \frac{AC}{AB}$

以及 $Sin Q = \frac{PR}{PQ}$

这意味着，

$\frac{AC}{AB} =  \frac{PR}{PQ}$

$\frac{AC}{PR} =  \frac{AB}{PQ}$

设$\frac{AC}{PR} =  \frac{AB}{PQ} = k$

$AC = k(PR)$ 以及 $AB = k(PQ)$

在三角形ABC和PQR中，使用勾股定理，

$AC^2 + BC^2 = AB^2$ 以及 $QR^2+PR^2=PQ^2$

$BC = \sqrt{(AB^2-AC^2)}$ 以及 $QR = \sqrt{(PQ^2-PR^2)}$

$\frac{BC}{QR} = \frac{ \sqrt{(AB^2-AC^2)}}{\sqrt{(PQ^2-PR^2)}}$

$\frac{BC}{QR} = \frac{ \sqrt{(kPQ)^2-(kPR^2)}}{\sqrt{(PQ^2-PR^2)}}$

$\frac{BC}{QR} = \frac{ \sqrt{k^2 (PQ^2-PR^2)}}{\sqrt{(PQ^2-PR^2)}}$

$\frac{BC}{QR} = \frac{k \sqrt{(PQ^2-PR^2)}}{\sqrt{(PQ^2-PR^2)}}$

$\frac{BC}{QR} = k$

$\frac{AC}{PR} = \frac{AB}{PQ} = k$ 以及 $\frac{BC}{QR} = k$

$\frac{AC}{PR} = \frac{AB}{PQ} = \frac{BC}{QR}$

在三角形ABC和PQR中，

$\frac{AC}{PR} = \frac{AB}{PQ} = \frac{BC}{QR}$

因此，

$∆ ACB ~ ∆ PRQ$

这意味着，

$∠ B = ∠ Q$。

证毕。

教程点

更新于: 2022年10月10日

160 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习