在△ABC和△DEF中，已知：AB = 5 cm，BC = 4 cm，CA = 4.2 cm；DE = 10 cm，EF = 8 cm，FD = 8.4 cm。如果AL ⊥ BC且DM ⊥ EF，求AL：DM。

已知

$AB = 5\ cm, BC = 4\ cm$ 和 $CA = 4.2\ cm; DE = 10\ cm, EF = 8\ cm$ 和 $FD = 8.4\ cm$.

$AL \perp BC$ 和 $DM \perp EF$。
要求：
 我们要求出 $AL : DM$。

解答

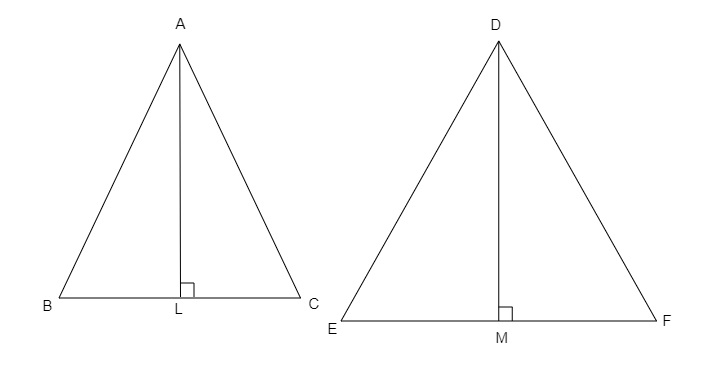
在△ABC和△DEF中，

$\frac{AB}{DE}=\frac{5}{10}=\frac{1}{2}$

$\frac{AC}{DF}=\frac{4.2}{8.4}=\frac{1}{2}$

$\frac{BC}{EF}=\frac{4}{8}=\frac{1}{2}$

$\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}$

因此，

根据SSS相似性，

△ABC ~ △DEF

这意味着，

∠C=∠F

在△ALC和△DMF中，

∠ALC=∠DMF=90°

∠C=∠F

因此，

△ALC ~ △DMF

这意味着，

$\frac{AC}{DF}=\frac{AL}{DM}$

$\frac{AL}{DM}=\frac{1}{2}$

$AL:DM=1:2$。

教程点

更新于： 2022年10月10日

56 次浏览

开启您的职业生涯

通过完成课程获得认证

开始学习