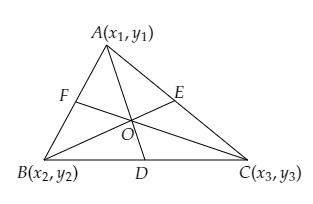
点 $A (x_1, y_1)$、$B (x_2, y_2)$ 和 $C (x_3, y_3)$ 是 $\triangle ABC$ 的顶点。
从 $A$ 出发的中线与 $BC$ 相交于点 $D$。求点 $D$ 的坐标。

已知

点 $A (x_1, y_1)$、$B (x_2, y_2)$ 和 $C (x_3, y_3)$ 是 $\triangle ABC$ 的顶点。

从 $A$ 出发的中线与 $BC$ 相交于点 $D$。

要求

我们需要求出点 $D$ 的坐标。

解答

$D$ 是 BC 的中点。

这意味着，

使用中点公式，我们得到：

点 $D$ 的坐标为 $(\frac{x_2+x_3}{2}, \frac{y_2+y_3}{2})$。

点 $D$ 的坐标为 $(\frac{x_2+x_3}{2}, \frac{y_2+y_3}{2})$。

教程点

更新于: 2022年10月10日

31 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习