什么是DFA的最小化?
问题
给定一个确定性有限自动机(DFA),尝试通过去除不可达状态和去除类似行来简化DFA。
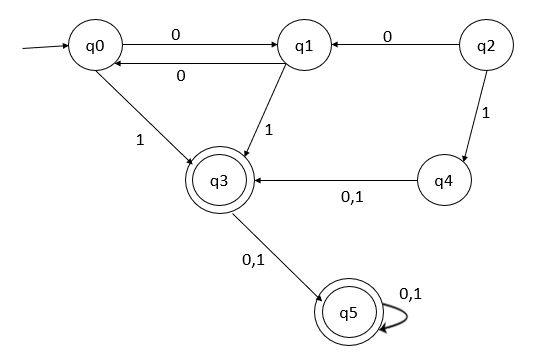
解决方案
步骤 1
从q0中移除不可达状态
从初始状态开始,我们无法到达q2和q4。因此,删除这两个状态,如下所示:
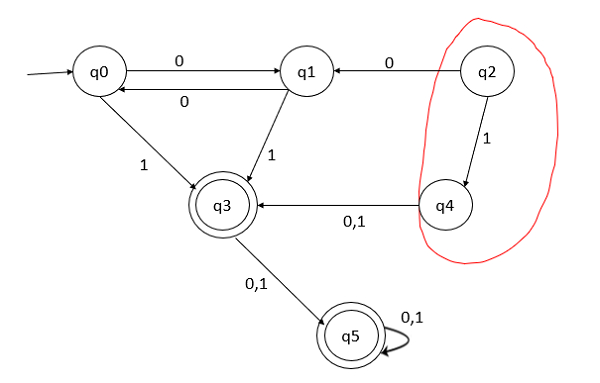
移除不可达状态后,部分最小化的DFA如下:
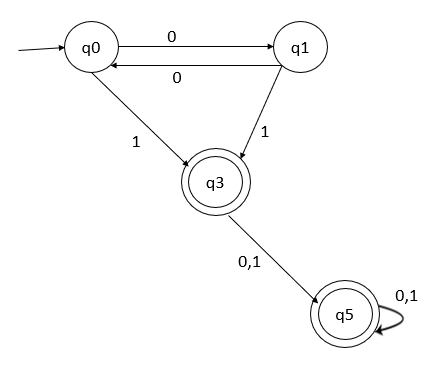
步骤 2
下面给出状态转换表:
| 状态 | 0 | 1 |
|---|---|---|
| ->q0 | q1 | q3 |
| q1 | q0 | q3 |
| *q3 | q5 | q5 |
| *q5 | q5 | q5 |
步骤 3
将表格划分为2个表格,如下所示:
表1从非终结状态开始。
| 状态 | 0 | 1 |
|---|---|---|
| ->q0 | q1 | q3 |
| q1 | q0 | q3 |
表2从终结状态开始。
| 状态 | 0 | 1 |
|---|---|---|
| *q3 | q5 | q5 |
| *q5 | q5 | q5 |
步骤 4
删除类似的行。
表1没有类似的行
表2有类似的行。因此,跳过q5并用q3替换q5
| 状态 | 0 | 1 |
|---|---|---|
| q3 | q5 | q3 |
步骤 5
合并两个表格,如下所示:
| 状态 | 0 | 1 |
|---|---|---|
| ->q0 | q1 | q3 |
| q1 | q0 | q3 |
| *q3 | q3 | q3 |
因此,最小化的DFA如下:
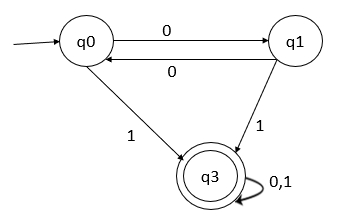

广告

 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP