数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
已知：同时掷两个骰子，一个蓝色，一个灰色。一名学生认为有 11 种可能的结果 2、3、4、5、6、7、8、9、10、11 和 12。因此，每种结果的概率为 $\frac{1}{11}$。需要解决的问题：我们需要确定学生的论点是正确还是错误。解答：当同时掷两个骰子（一个蓝色，一个绿色）时，总共有 $6 \times 6=36$ 种可能的结果这意味着，可能结果的总数 $n=36$。当两个骰子的点数之和为 2 时，可能的结果是 (1, 1)有利结果的数量 ... 阅读更多
已知：一个游戏包括掷一枚一卢比硬币 3 次，并每次记录其结果。如果三次投掷都得到相同的结果，即三个正面或三个反面，哈尼夫获胜，否则失败。需要解决的问题：我们需要计算哈尼夫输掉比赛的概率。解答：掷一枚硬币三次时，可能的结果为 $HHH, TTT, HHT, HTH, THH, TTH, THT, HTT$这意味着，可能结果的总数 $n=8$。三次投掷都得到相同结果的结果数 = 2这意味着，有利结果的数量 = $8-2=6$我们知道，事件的概率 = $\frac{有利结果的数量}{可能结果的总数}$因此，哈尼夫输掉比赛的概率 ... 阅读更多
已知：掷骰子两次。需要解决的问题：我们需要找到 (i) 两次都不出现 5 的概率。(ii) 5 至少出现一次的概率。解答：当掷骰子两次时，可能的总结果为 $6\times6=36$。这意味着，可能结果的总数 $n=36$(i) 两次都不出现 5 的结果为 $(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 6), $$(4, 1), (4, 2), (4, 3), (4, 4), (4, 6), (6, 1), (6, 2), ... 阅读更多
已知：掷骰子两次。需要解决的问题：我们需要找到 5 至少出现一次的概率。解答：当掷骰子两次时，可能的总结果为 $6\times6=36$。这意味着，可能结果的总数 $n=36$。5 至少出现一次的结果为 $(1, 5), (2, 5), (3, 5), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 5)$5 至少出现一次的结果数 = 11有利结果的总数 = 11事件的概率 = $\frac{有利结果的数量}{可能结果的总数}$因此，5 至少出现一次的概率 ... 阅读更多
已知：如果同时抛掷两枚硬币，则有三种可能的结果：两个正面、两个反面或一个正面一个反面。因此，每种结果的概率为 $\frac{1}{3}$。需要解决的问题：我们需要确定给定的陈述是真还是假。解答：(i) 当同时抛掷两枚硬币时，可能的结果为 HH、HT、TH 和 TT。这意味着，可能结果的总数 $n=4$。我们知道，事件的概率 = $\frac{有利结果的数量}{可能结果的总数}$因此，得到两个正面的概率 = $\frac{1}{4}$得到两个反面的概率 = $\frac{1}{4}$得到一个正面和一个反面的概率 = $\frac{2}{4}=\frac{1}{2}$因此，给定的 ... 阅读更多
已知：如果掷一个骰子，则有两种可能的结果：奇数或偶数。因此，得到奇数的概率为 $\frac{1}{2}$。需要解决的问题：我们需要确定给定的陈述是真还是假。解答：当掷一个骰子时，可能的结果为 1、2、3、4、5 和 6。这意味着，可能结果的总数 $n=6$。我们知道，事件的概率 = $\frac{有利结果的数量}{可能结果的总数}$因此，得到奇数的概率 = $\frac{3}{6}=\frac{1}{2}$因此，给定的陈述是正确的。
已知：两位顾客在同一周（周二到周六）访问一家特定商店。每个人在任何一天访问商店的可能性都相同。需要解决的问题：我们需要找到这两位顾客都将在哪天访问商店的概率。(i) 同一天(ii) 连续几天(iii) 不同的几天解答：从周二到周六的天数 = 5这意味着，可能结果的总数 $n=5\times5=25$。(i) 两位顾客都在同一天访问商店的结果数 = 5有利结果的总数 = 5。我们知道，事件的概率 = $\frac{有利结果的数量}{可能结果的总数}$因此，这两位顾客都将在 ... 阅读更多
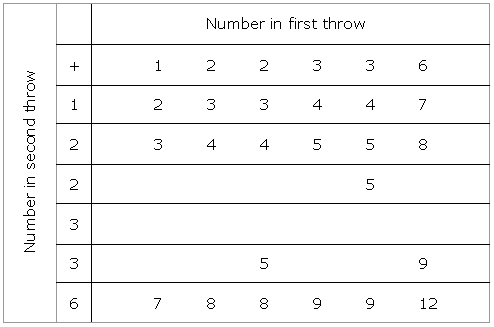
已知：一个骰子的每一面分别标有数字 1、2、2、3、3、6。掷骰子两次，并记录两次投掷的总点数。需要解决的问题：我们需要找到两次投掷总点数为以下数值的概率：(i) 偶数(ii) 6(iii) 至少 6解答：要完成给定的表格，我们只需要将每一面的数字相加即可。当掷两个骰子时，可能的总结果为 $6\times6=36$。所有可能的结果为 $(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), ... 阅读更多
**已知：** 一批钢笔共有 144 支，其中 20 支有缺陷，其余为合格品。努丽如果买到的是合格品就会购买，但如果买到的是有缺陷的则不会购买。店主随机抽取一支钢笔给她。**要求：** 我们需要求出以下概率：(i) 她会购买这支钢笔。(ii) 她不会购买这支钢笔。**解答：**钢笔总数 = 144 支这意味着，可能出现的结果总数 n = 144。(i) 有缺陷的钢笔数 = 20 支合格钢笔数 = 144 - 20 = 124 支有利结果总数（她会购买）= 124 支。我们知道，事件的概率 = 有利结果数 / 可能结果总数。 ... 阅读更多
**已知：** 同时掷出两个骰子，一个蓝色，一个灰色。一名学生认为有 11 种可能的结果：2、3、4、5、6、7、8、9、10、11 和 12。因此，每种结果的概率都是 1/11。**要求：** 我们需要：(i) 完成给定的表格。(ii) 判断该学生的论点是否正确。**解答：**当同时掷出两个骰子（一个蓝色，一个灰色）时，可能出现的结果总数 = 6 × 6 = 36这意味着，可能出现的结果总数 n = 36。(i) 当两个骰子上的点数之和 = 2 时，可能的结果是 ... 阅读更多