数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学
已知：一个袋子只装有柠檬味糖果。玛丽尼不看袋子拿出一个糖果。要求：我们必须找到她拿出 (i) 橙味糖果 (ii) 柠檬味糖果 的概率解答：(i) 已知袋子只装有柠檬味糖果。这意味着，袋中橙味糖果的数量 = 0 总共可能的事件数 = 0。我们知道，事件概率 = 有利事件数 / 总共可能的事件数 因此，她拿出橙味糖果的概率 = 0 / 总共可能的事件数 = 0 她拿出橙味糖果的概率是 0。(ii) 已知袋子只装有柠檬味……阅读更多
已知：一个袋子装有 3 个红球和 5 个黑球。从袋子中随机抽取一个球。要求：我们必须找到抽到的球是 (i) 红球 (ii) 不是红球 的概率解答：(i) 红球数量 = 3 黑球数量 = 5 球的总数 = 3 + 5 = 8 这意味着，总共可能的事件数 n = 8。有利事件数（抽到红球）= 3。我们知道，事件概率 = 有利事件数 / 总共可能的事件数 因此，抽到红球的概率 = 3/8 抽到红球的概率是 3/8。(ii) 红球数量 = 3 黑球数量……阅读更多
已知：一个盒子装有 5 个红弹珠，8 个白弹珠和 4 个绿弹珠。从盒子里随机取出一个弹珠。要求：我们必须找到取出的是 (i) 红弹珠 (ii) 白弹珠 (iii) 不是绿弹珠 的概率解答：红弹珠数量 = 5 白弹珠数量 = 8 绿弹珠数量 = 4 弹珠总数 = 5 + 8 + 4 = 17 这意味着，总共可能的事件数 n = 17。(i) 有利事件数（取出红弹珠）= 5。我们知道，事件概率 = 有利事件数 / 总共可能的事件数 因此，取出红弹珠的概率 = 5/17 取出……阅读更多
已知：一个存钱罐里有一百枚 50 分的硬币，五十枚 1 元的硬币，二十枚 2 元的硬币和十枚 5 元的硬币。如果硬币掉出来的可能性相同。要求：我们必须找到硬币不是 5 元硬币的概率。解答：存钱罐里硬币的总数 = 100 + 50 + 20 + 10 = 180 令 E 为得到 5 元硬币的事件。可能的事件数 = 180 有利于事件 E 的事件数 = 10 因此 P(E) = 有利事件数 / 总共可能的事件数 = 10/180 = 1/18 因此……阅读更多
"
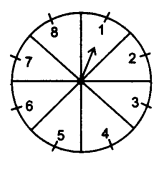
已知：一个机会游戏包括旋转一个箭头，箭头最终指向 1、2、3、4、5、6、7、8 中的一个数字，这些结果的可能性相同。要求：我们必须找到指向 (i) 8 (ii) 奇数 (iii) 大于 2 的数字 (iv) 小于 9 的数字 的概率解答：给出数字 1, 2, 3,…,8。这意味着，总共可能的事件数 n = 8。(i) 有利事件数（指向 8）= 1。我们知道，事件概率 = 有利事件数 / 总共可能的事件数 因此，……阅读更多
下表显示了一些世界顶级击球手在一对一国际板球比赛中取得的进球数。
| 进球数 | 击球手数量 | 进球数 | 击球手数量 |
| 3000-4000 | 4 | 7000-8000 | 6 |
| 4000-5000 | 18 | 8000-9000 | 3 |
| 5000-6000 | 9 | 9000-10000 | 1 |
| 6000-7000 | 7 | 10000-11000 | 1 |
求数据的中位数。
已知：下表显示了一些世界顶级击球手在一对一国际板球比赛中取得的进球数。要求：我们必须找到数据的中位数。解答：给定数据的频率如下所示。进球数（xi）：击球手数量（fi）：3000-4000 4 4000-5000 18 5000-6000 9 6000-7000 7 7000-8000 6 8000-9000 3 9000-10000 1 10000-11000 1 我们观察到 4000-5000 的区间频率最大（18）。因此，它是众数区间。这里，l=4000，h=1000，f=18，f1=4，f2=9 我们知道，众数 = l + (f - f1) / (2f - f1 - f2) * h = 4000 + (18 - 4) / (2 * 18 - 4 - 9) * 1000 = 4000 + 14 / (36 - 13) * 1000 = 4000 + 14000 / 23 = 4000 + 608.7 = 4608.7 给定数据的中位数是 4608.7。阅读更多
已知：给定分布的中位数为 28.5。总频数为 60。要求：我们必须找到 x 和 y 的值。解：中位数 = 28.5，N = 60 x + y = 60 - (5 + 20 + 15 + 5) x + y = 60 - 45 = 15 y = 15 - x ……….(i)以下是给定数据的累积频率 (CF) 表：组距累积频数(CF)0-10 5 510-20 x 5 + x20-30 20 25 + x30-40 15 40 + x40-50 y 40 + x + y50-60 5 45 + x + y这里，观察数 (n) = 60所以，n/2 = 30由于中位数为 28.5，因此中位数组为 20-30因此，l = 20，h = 10，f = 20，cf = 5 + x。因此，中位数 = ... 阅读更多
一株植物的 40 片叶子的长度精确到最接近的毫米进行测量，得到的数据如下表所示
| 长度（毫米） | 118-126 | 127-135 | 136-144 | 145-153 | 154-162 | 163-171 | 172-180 |
| 叶子的数量 | 3 | 5 | 9 | 12 | 5 | 4 | 2 |
求叶子的中位长度。
（提示：由于公式假设连续组距，因此需要将数据转换为连续组距才能找到中位数。然后组距变为 117.5 – 126.5）
已知：一株植物的 40 片叶子的长度精确到最接近的毫米进行测量。要求：我们必须找到叶子的平均长度。解：将组距排列成互斥形式，然后形成其累积频率表，如下所示：这里，N = 40 N/2 = 40/2 = 20累积频率刚好大于 N/2 的值为 29，对应的组距为 144.5 – 153.5。这意味着 144.5 – 153.5 是中位数组距。因此，l = 144.5，f = 12，F = 17，h = (153.5 - 144.5) = 9中位数 = l + (N/2 - F)/f × h = 144.5 + (20 - 17)/12 × 9 = 144.5 + 3/4 × 3 = 144.5 + 9/4 = 144.5 + ... 阅读更多
下表列出了 400 个霓虹灯的寿命分布
寿命：（小时） | 灯的数量 |
| 1500-2000 | 14 |
| 2000-2500 | 56 |
| 2500-3000 | 60 |
| 3000-3500 | 86 |
| 3500-4000 | 74 |
| 4000-4500 | 62 |
| 4500-5000 | 48 |
求灯的中位寿命。
已知：下表列出了 400 个霓虹灯的寿命分布。要求：我们必须找到中位寿命。解：这里，N = 400 N/2 = 400/2 = 200累积频率刚好大于 N/2 的值为 216，对应的组距为 3000 – 3500。这意味着 3000 – 3500 是中位数组距。因此，l = 3000，f = 86，F = 130，h = (3500 - 3000) = 500中位数 = l + (N/2 - F)/f × h = 3000 + (200 - 130)/86 × 500 = 3000 + 70/86 × 500 = 3000 + 35000/86 = 3000 + 406.98 = 3406.98中位寿命为 3406.98 小时。
从本地电话簿中随机抽取了 100 个姓氏，并获得了姓氏中英文字母数量的频率分布如下所示
| 字母数量 | 1-4 | 4-7 | 7-10 | 10-13 | 13-16 | 16-19 |
| 姓氏数量 | 6 | 30 | 40 | 16 | 4 | 4 |
确定姓氏中字母的中位数。求姓氏中字母的平均数。还
已知：从本地电话簿中随机抽取了 100 个姓氏，并获得了姓氏中英文字母数量的频率分布如下所示。要求：我们必须确定姓氏中字母的中位数和平均数，并找到姓氏的众数大小。解：给定数据的频率如下所示。设假设平均值为 A=8.5。我们知道，平均值 = A + Σfidᵢ/Σfᵢ因此，平均值 = 8.5 + (-18/100) = 8.5 - 0.18 = 8.32给定数据的平均值为 8.32。我们观察到 7-10 组距具有最大频率 (40)。因此，它是… 阅读更多