数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
一个 1.2 米高的女孩发现一个气球在水平线上随风飘动，气球距离地面 88.2 米。在某一时刻，女孩的眼睛到气球的仰角为 60°。过了一段时间，仰角降至 30°（见图）。求这段时间内气球移动的距离。
"
已知：一个 1.2 米高的女孩发现一个气球在水平线上随风飘动，气球距离地面 \( 88.2 \mathrm{~m} \) 。在某一时刻，女孩的眼睛到气球的仰角为 \( 60^{\circ} \) 。过了一段时间，仰角降至 \( 30^{\circ} \) 。要求：我们需要找到这段时间内气球移动的距离。 解决方案：设 x 为女孩最初与气球之间的水平距离，y 为女孩最终与气球之间的水平距离。因此，最初 \(\tan\ 60^o=\frac{88.2-1.2}{x}\) \(\sqrt3=\frac{87}{x}\) \(x=\frac{87}{\sqrt3}\) \(x=\frac{87\sqrt3}{\sqrt3\times\sqrt3}\) \(x=\frac{87\sqrt3}{3}\) \(x=29\sqrt3\) 最终，... 阅读更多
已知：一个 \( 1.5 \mathrm{~m} \) 高的男孩站在距离一栋 \( 30 \mathrm{~m} \) 高的建筑物一定距离的地方。他眼睛到建筑物顶部的仰角从 \( 30^{\circ} \) 增加到 \( 60^{\circ} \) ，当他走向建筑物时。要求：我们需要找到他朝建筑物方向行走的距离。解决方案：\(\mathrm{AB}\) 是男孩的身高，\(\mathrm{CD}\) 是建筑物的高度。从图中，\(\mathrm{AB}=\mathrm{OP}=\mathrm{DE}=1.5 \mathrm{~m}, \angle \mathrm{CAE}=30^{\circ}, \angle \mathrm{COE}=60^{\circ}\) 设他朝建筑物方向行走的距离为 \(\mathrm{AO}=x \mathrm{~m}\)。这意味着，\(\mathrm{CE}=30-1.5=28.5 \mathrm{~m}\) 我们知道，\(\tan \theta=\frac{\text { 对边 }}{\text { 邻边 }}\) ... 阅读更多
已知：从地面上的一点，观察到固定在 \( 20 \mathrm{~m} \) 高建筑物顶部的发射塔的底部和顶部的仰角分别为 \( 45^{\circ} \) 和 \( 60^{\circ} \) 。要求：我们需要找到发射塔的高度。解决方案：\(\mathrm{AB}\) 是高建筑物，\(\mathrm{BC}\) 是发射塔的长度。设 D 为观察点。从图中，\(\mathrm{AB}=20 \mathrm{~m}, \angle \mathrm{BDA}=45^{\circ}, \angle \mathrm{CDA}=60^{\circ}\) 设发射塔的高度为 \(\mathrm{BC}=h \mathrm{~m}\)，观察点与建筑物底部之间的距离为 ... 阅读更多
已知：一座 \( 1.6 \mathrm{~m} \) 高的雕像矗立在一个底座的顶部。从地面上的一点，观察到雕像顶部的仰角为 \( 60^{\circ} \)，从同一点观察到底座顶部的仰角为 \( 45^{\circ} \) 。要求：我们需要找到底座的高度。解决方案：\(\mathrm{AB}\) 是底座的高度，\(\mathrm{BC}\) 是雕像的高度。设 D 为观察点。从图中，\(\mathrm{BC}=1.6 \mathrm{~m}, \angle \mathrm{CDA}=60^{\circ}, \angle \mathrm{BDA}=45^{\circ}\) 设底座的高度为 \(\mathrm{AB}=h \mathrm{~m}\)，观察点与 ... 阅读更多
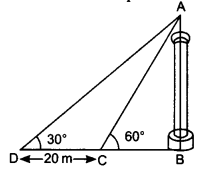
已知：从塔底到建筑物顶部的仰角为 \( 30^{\circ} \)，从建筑物底到塔顶的仰角为 \( 60^{\circ} \) 。塔高 \( 50 \mathrm{~m} \) 。要求：我们需要找到建筑物的高度。解决方案：\(\mathrm{AB}\) 是塔的高度，\(\mathrm{CD}\) 是建筑物的高度。从图中，\(\mathrm{AB}=50 \mathrm{~m}, \angle \mathrm{BCA}=60^{\circ}, \angle \mathrm{DAC}=30^{\circ}\) 设建筑物的高度为 \(\mathrm{CD}=h \mathrm{~m}\)，建筑物与塔之间的距离为 \(\mathrm{CA}=x \mathrm{~m}\)。我们知道， ... 阅读更多
"
已知：一个电视塔垂直矗立在运河的一岸。从对岸与塔底正对的一点，观察到塔顶的仰角为 60°。从与该点相距 20 米的另一点（该点在线段上，连接该点与塔底），观察到塔顶的仰角为 30°。要求：我们需要找到塔的高度和运河的宽度。解决方案：\(\mathrm{AB}\) 是塔的高度，\(\mathrm{BC}\) 是运河的宽度。设 C 为 ... 阅读更多
已知：从地面上一点到塔顶的仰角为 30°，该点距离塔底 30 米。要求：我们需要找到塔的高度。解决方案：在上图中，AB 代表塔，C 是距离塔底 30 米的一点，从点 C 观察到塔顶的仰角为 30°。设塔的高度为 h 米现在，在三角形 ABC 中，\(\tan\ 30^o\ =\ \frac{h}{30}\) \(\Rightarrow \ \frac{1}{\sqrt{3}} \ =\ \frac{h}{30}\) \(\Rightarrow \ h\ =\ \frac{30}{\sqrt{3} \ } \ =\ 10\sqrt{3}\) 因此，... 阅读更多
**已知：**一只风筝在离地面 60 米的高空飞行。系着风筝的线暂时系在地面上的一个点上。线与地面的倾角为 60°。
**已知：**一棵树因暴风雨折断，折断的部分弯曲，使树顶触地，与地面成 30° 角。树根到树顶触地点的距离为 8 米。
**已知：**一个承包商计划在公园里安装两个滑梯供孩子们玩耍。对于 5 岁以下的孩子，她希望滑梯顶部高度为 1.5 米，与地面成 30° 角；而对于年龄较大的孩子，她希望滑梯更陡峭，顶部高度为 3 米，与地面成 60° 角。