已知:三角形 $ABC$ 外接一个半径为 4 厘米的圆,且点 $D$ 与 $BC$ 相切,$BD$ 和 $DC$ 的长度分别为 8 厘米和 6 厘米。求解:我们需要求出边 $AB$ 和 $AC$ 的长度。解:假设圆分别与三角形的边 $AB$ 和 $AC$ 相切于点 $E$ 和 $F$,且线段 $AF$ 的长度为 $x$。$AE = AF = x\ cm$在 $∆ABC$ 中,$a = 6 + 8$$= 14\ cm$$b = (x + 6)\ cm$$c = (x + ... 阅读更多
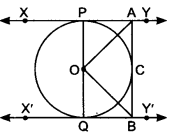
已知:$XY$ 和 $X’Y’$ 是圆 $x$ 的两条平行切线,圆心为 $O$,另一条切线 $AB$ 与切点 $C$ 相交于 $XY$ 的 $A$ 点和 $X'Y'$ 的 $B$ 点。求解:我们需要证明 $\angle AOB=90^{o}$。解:$XY$ 和 $X'Y'$ 是圆心为 $O$ 的圆的两条平行切线,分别与圆相切于 $P$ 点和 $Q$ 点。$AB$ 是切点为 $C$ 的切线,与 $XY$ 相交于 $A$ 点,与 $X'Y'$ 相交于 $B$ 点。步骤如下:连接 $OC$。在 $\vartriangle OAP$ 和 $\vartriangle OAC$ 中,$OP=OC\ \ \ \ \ \ \ \ \ ( 圆的半径)$$AP =AC\ \ \ ... 阅读更多
求解:我们需要证明从圆外一点到圆的两条切线之间的夹角与连接切点在圆心处所成的角互补。解:假设 $PA$ 和 $PB$ 是两条切线,$A$ 和 $B$ 是切点的坐标。$\mathrm{OA} \perp \mathrm{AP}$$\mathrm{OB} \perp \mathrm{BP}$$\angle \mathrm{OAP}=\angle \mathrm{OBP}=90^{\circ}$在四边形 $\mathrm{OAPB}$ 中$\angle \mathrm{OAP}+\angle \mathrm{OBP}+\angle \mathrm{APB}+\angle \mathrm{AOB}=360^{\circ}$$90^{\circ}+90^{\circ}+\angle \mathrm{APB}+\angle \mathrm{AOB}=360^{\circ}$$\angle \mathrm{APB}+\angle \mathrm{AOB}=360^{\circ}-180^{\circ}$$=180^{\circ}$因此,$\angle \mathrm{APB}$ 和 $\angle \mathrm{AOB}$ 是互补角。证毕。 阅读更多
正确答案:(c) (a)-(ii), (b)-(i), (c)-(iii)解释:尼龙 = 纤维,PVC = 热塑性塑料,酚醛树脂 = 热固性塑料
已知:两个同心圆的半径分别为 \( 5 \mathrm{~cm} \) 和 \( 3 \mathrm{~cm} \)。求解:我们需要求出较大圆的弦长,该弦与较小圆相切。解:设 $R$ 为外圆的半径,$r$ 为两个同心圆的内圆的半径。$AB$ 是外圆的弦,与内圆相切于 $P$ 点。连接 $OP$ 和 $OA$。这意味着,$OP\ \perp\ AB$ 且平分 $AB$ 于 $P$ 点。$OA=R$ 且 $OP=r$$OA=5\ cm$ $OP=3\ cm$在直角三角形 $OAP$ 中,$AP=\sqrt{OA^{2}-OP^{2}}$$=\sqrt{5^{2}-3^{2}}$$=\sqrt{25-9}$$=\sqrt{16}$$=4\ cm$$AB=2AP$$=2 \times 4\ cm$$=8\ cm$较大圆的弦长为 ... 阅读更多
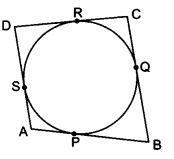
已知:一个四边形 $ABCD$ 外接一个圆。求解:我们需要证明 $AB\ +\ CD\ =\ AD\ +\ BC$。解:由于从外一点到圆的两条切线长度相等,$AP\ =\ AS\ \dotsc .( 1)$$BP\ =\ BQ\ \dotsc .( 2)$$CR\ =\ CQ\ \dotsc .( 3)$$DR\ =\ DS\ \dotsc .( 4)$将等式 $( 1) ,\ ( 2) ,\ ( 3)$ 和 $( 4)$ 相加,得到$AP\ +\ BP\ +\ CR\ +\ DS\ =\ AS\ +\ BQ\ +\ CQ\ +\ DS$$\therefore \ ( AP\ +\ BP) \ +\ ( CR\ +\ DR) \ =\ ( AS\ +\ DS) \ +\ ( BQ\ +\ CQ)$$\therefore \ AB\ +\ CD\ =\ AD\ +\ BC$证毕。
求解:我们需要证明在圆的直径两端画出的切线是平行的。解:假设 $AB$ 是圆的直径,$p$ 和 $q$ 是两条切线。$OA \perp p$$OB \perp q$$\angle 1 = \angle 2 = 90^o$这意味着,$p \| q$ (垂直于同一条直线的两条直线互相平行)证毕。
求解:我们需要证明与圆的切线在切点处的垂线经过圆心。解:假设 $TS$ 是圆心为 $O$,切点为 $P$ 的切线。连接 $OP$。画一条线 $OR$,与圆相交于 $Q$ 点,并与切线 $TS$ 相交于 $R$ 点。$OP = OQ$ (圆的半径)$OQ $\Rightarrow OP 同样,$OP$ 小于从 $O$ 到 $TS$ 的所有其他线段。$OP$ 是最短的线段。因此,$OP$ 垂直于 $TS$。经过 $P$ 的垂线将穿过圆心。证毕。 阅读更多
已知:从距离圆心 5 厘米的点 $A$ 到圆的切线长度为 4 厘米。求解:我们需要求出圆的半径。解:设 OP 为圆的半径。$OAP$ 是一个直角三角形。因此,$OA^2=AP^2+OP^2$$5^{2}=4^{2}+\mathrm{OP}^{2}$25=16+\mathrm{OP}^{2}$$\mathrm{OP}^{2}=25-16$$\mathrm{OP}^{2}=9$ $\mathrm{OP}=\sqrt{9}$$\mathrm{OP}=3 \mathrm{~cm}$圆的半径为 $3 \mathrm{~cm}$。
**已知:**从点P到圆心为O的圆的两条切线PA和PB彼此倾斜角为80°。**求:**∠POA。**解:**我们知道,圆的切线垂直于过切点的半径。从外一点引出的切线长相等。这意味着,在△OAP和△OBP中,OA = OBPA = PBOP = OP因此,根据SSS全等,△OAP ≅ △OBP这意味着,∠AOB + ∠APB = 180°∠AOB + 80° = 180°∠AOB = 180° - 80°∠AOB = 100°这意味着,∠ ... 阅读更多

 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP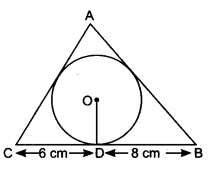 "
"

 "
"

 "
"