数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
任务：我们需要求出：(i) 点 D 的坐标。(ii) 求 $AD$ 上一点 $P$ 的坐标，使得 $AP : PD = 2 : 1$。(iii) 求中线 $BE$ 和 $CF$ 上的点 $Q$ 和 $R$ 的坐标，使得 $BQ : QE = 2 : 1$ 且 $CR : RF = 2 : 1$。(iv) 我们观察到什么[注意：三条中线交于一点，该点称为重心，并且该点将每条中线分成 2: 1 的比例](v) 如果 $A(x_1, y_1), B(x_2, y_2)$ 和 $C(x_3, y_3)$ 是 ... 阅读更多
已知：三角形的顶点为 $(0, -1), (2, 1)$ 和 $(0, 3)$。任务：我们需要求出连接三角形各边的中点的三角形的面积，以及该面积与给定三角形面积的比值。解答：设 $\mathrm{D}, \mathrm{E}$ 和 $\mathrm{F}$ 分别为三角形 $\mathrm{ABC}$ 的边 $\mathrm{AB}, \mathrm{BC}$ 和 $\mathrm{AC}$ 的中点。这意味着，点 $ \mathrm{D}$ 的坐标 $=\frac{0+2}{2}, \frac{-1+1}{2}$$=(1, 0)$点 $\mathrm{E}$ 的坐标 $=\frac{2+0}{2}, \frac{1+3}{2}$$=(1, 2)$点 $\mathrm{F}$ 的坐标 $=\frac{0+0}{2}, \frac{3-1}{2}$$=(0, 1)$三角形 $\mathrm{DEF}$ 的面积 $=\frac{1}{2}[1(2-1)+1(1-0)+0(0-2)]$$=\frac{1}{2}[1+1+0]$$=\frac{2}{2}$$=1$ 平方单位。三角形 $\mathrm{ABC}$ 的面积 $=\frac{1}{2}[0(1-3)+2(3+1)+0(-1-1)]$$=\frac{1}{2}[0+8+0]$$=4$ 平方单位面积的比值 ... 阅读更多
已知：四边形的顶点为 $(-4, -2), (-3, -5), (3, -2), (2, 3)$。任务：我们需要求出四边形的面积。解答：设 $A (-4, -2), B (-3, -5), C(3, -2)$ 和 $D (2, 3)$ 为四边形 $ABCD$ 的顶点。连接 $A$ 和 $C$ 得到两个三角形 $ABC$ 和 $ADC$。这意味着，四边形 $ABCD$ 的面积 = 三角形 $ABC$ 的面积 + 三角形 $ADC$ 的面积。我们知道，顶点为 $(x_1, y_1), (x_2, y_2), (x_3, y_3)$ 的三角形的面积由下式给出： 三角形面积 $=\frac{1}{2}[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]$因此，三角形 $ABC$ 的面积 $=\frac{1}{2}[-4(-5+2)+(-3)(-2+2)+3(-2+5)]$$=\frac{1}{2}[-4(-3)+(-3)0+3(3)]$$=\frac{1}{2}[12+9]$$=\frac{1}{2} \times 21$$=\frac{21}{2}$ 平方单位。三角形 $ADC$ 的面积 $=\frac{1}{2}[-4(-2-3)+2(-2+2)+3(3+2)]$$=\frac{1}{2}[-4(-5)+2(0)+3(5)]$$=\frac{1}{2}[20+0+15]$$=\frac{1}{2} \times 35$$=\frac{35}{2}$ 平方单位。因此， ... 阅读更多
已知：三角形的顶点为 $A (4, -6), B (3, -2)$ 和 $C (5, 2)$。任务：我们需要证明三角形的中线将其分成两个面积相等的三角形。解答：设 $A (4, -6), B (3, -2)$ 和 $C (5, 2)$ 为三角形 $ABC$ 的顶点。设 $D$ 为 $\triangle ABC$ 的边 $BC$ 的中点。这意味着，点 $D$ 的坐标 = BC 的中点 $= (\frac{3+5}{2}, \frac{-2+2}{2})$$=(\frac{8}{2}, 0)$$=(4, 0)$$AD$ 是 $\triangle ABC$ 的中线。三角形 $\mathrm{ABD}$ 的面积 $=\frac{1}{2}[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]$$=\frac{1}{2}[4 \times(-2-0)+3(0+6)+4(-6+2)]$$=\frac{1}{2}[-8+18-16]$$=\frac{-6}{2}$ $=3$ 平方单位 三角形 $\mathrm{ADC}$ 的面积 $=\frac{1}{2}[4(0-2)+4(2+6)+5\times(-6-0)]$$=\frac{1}{2}[-8+32-30]$$=\frac{-6}{2}$$=3$ 平方单位三角形 $\mathrm{ABD}$ 的面积 = 三角形 $\mathrm{ADC}$ 的面积因此， ... 阅读更多
已知：一点将连接点 $(-1, \ 7)$ 和 $(4, \ -3)$ 的线段按 $2 : 3$ 的比例分成两段。任务：我们需要求出该点的坐标。解答：设 $P(x, y)$ 为将连接给定点线段内部分成的点的坐标。这里，$x_1=-1, \ y_1=7, \ x_2=4, \ y_2=-3, \ m=2$ 且 $n=3$。使用分点公式，$( x, \ y)=( \frac{mx_2+nx_1}{m+n}, \ \frac{my_2+ny_1}{m+n})$$P( x, \ y)=( \frac{2\times4+3\times(-1)}{2+3}, \ \frac{2\times(-3)+3\times7}{2+3})$$(x, \ y)=( \frac{8-3}{5}, \ \frac{-6+21}{5})$$( x, \ y)=( \frac{5}{5}, \ \frac{15}{5})$$(x, \ y)=(1, 3)$因此，$( 1, \ 3)$ 将连接 ... 阅读更多
已知：给定点为 $(4, -1)$ 和 $(-2, -3)$。任务：我们需要求出连接给定点的线段的三等分点的坐标。解答：设端点为 $A (4, -1)$ 和 $B (-2, -3)$ 的线段在点 $C(x_1, y_1)$ 和 $D(x_2, y_2)$ 处被三等分。$C$ 将线段按 $1 : 2$ 的比例分成两段这意味着，$AC : CB = 1 : 2$因此，使用分点公式$(x, y)=[\frac{m x_{2}+n x_{1}}{m+n}, \frac{m y_{2}+n y_{1}}{m+n}]$$C(x_1, y_1)=\frac{1 \times(-2)+2 \times 4}{1+2}, \frac{1 \times (-3)+2 \times(-1)}{1+2}$$=(\frac{-2+8}{3}, \frac{-3-2}{3})$ $=(\frac{6}{3}, \frac{-5}{3})$$=(2, \frac{-5}{3})$$D$ 将 $AB$ 按 $2: 1$ 的比例分成两段这意味着，$A D: D B=2: 1$$D(x_2, ... 阅读更多
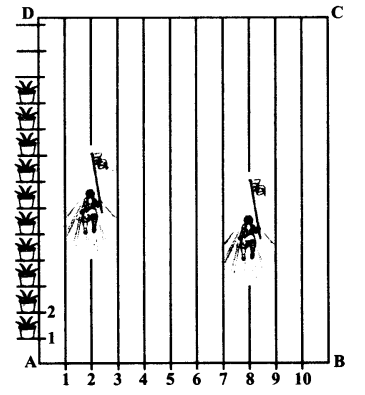
已知：为了举办运动会活动，在你们矩形形状的学校操场ABCD上，用粉笔画了距离每隔1米的一条线。在AD边上每隔1米放置了100个花盆。妮哈丽卡沿着第2条线跑了AD距离的$\frac{1}{4}$，并在那里插了一面绿旗。普利特沿着第8条线跑了AD距离的$\frac{1}{5}$，并在那里插了一面红旗。需要做：我们需要找到两面旗子之间的距离，以及如果拉什米需要在连接这两面旗子的线段的中点插一面蓝旗，... 阅读更多
已知：点$(-1, 6)$在连接点$(-3, 10)$和B$(6, -8)$的线段上。需要求：我们需要找到分割的比例。解：设点$(-1, 6)$将点$(-3, 10)$和$(6, -8)$按$m:n$内分。截距公式为$(x, y) = (\frac{m x_{2} + n x_{1}}{m + n} , \frac{m y_{2} + n y_{1}}{m + n})$设$P(x, y) = P(-1, 6)$；$A (x_{1}, y_{1}) = A(-3, 10)$；$B(x_{2}, y_{2}) = B(6, -8)$因此，$(-1, 6) = (\frac{m (6) + n(-3)}{m + n} , \frac{m (-8) + n (-3)}{m + n} )$比较可得，$-1 = \frac{6m-3n}{m + n}$$-1(m + ... 阅读更多
已知：连接点$A(1, -5)$和$B(-4, 5)$的线段被x轴分割。需要做：我们需要找到分割的比例和分割点的坐标。解：分割这条线段的点位于x轴上。这意味着，它的纵坐标为$0$。设点$P(x, 0)$按$m : n$的比例分割连接点$A(1, -5)$和$B(-4, 5)$的线段。使用截距公式，我们有$(x, y)=(\frac{mx_{2}+nx_{1}}{m+n}, \frac{my_{2}+ny_{1}}{m+n})$因此，$P(x, 0)=(\frac{m \times (-4)+n \times 1}{m+n}, \frac{m \times 5+n \times(-5)}{(m+n)})$$\Rightarrow \frac{5m-5n}{m+n}=0$$\Rightarrow 5m-5n=0$$\Rightarrow 5m=5n$$\Rightarrow \frac{m}{n}=\frac{5}{5}$$\Rightarrow m:n=1:1$这意味着，$x=\frac{1(-4)+1(1)}{1+1}$$=\frac{-4+1}{2}$$=\frac{-3}{2}$分割的比例为$1:1$，且... 阅读更多
已知：点$(1, 2), (4, y), (x, 6)$和$(3, 5)$是平行四边形的顶点，按顺序排列。需要做：我们需要找到$x$和$y$的值。解：设平行四边形的顶点为$A(1, 2), B(4, y), C(x, 6)$和$D(3, 5)$，且对角线$AC$和$BD$互相平分于点$O$。$O$是$AC$的中点。这意味着，使用中点公式，点$O$的坐标为$(\frac{x+1}{2}, \frac{6+2}{2})$$=(\frac{x+1}{2}, 4)$$O$也是$BD$的中点。这意味着，点$O$的坐标为$(\frac{4+3}{2}, \frac{y+5}{2})$$=(\frac{7}{2}, \frac{y+5}{2})$因此，$\frac{x+1}{2}=\frac{7}{2}$且$4=\frac{y+5}{2}$$\Rightarrow x+1=7$且$4(2)=y+5$$\Rightarrow x=7-1=6$且$y=8-5=3$$x$和$y$的值为... 阅读更多