数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
要做的：这里，我们需要写出问题 1 中给定的有理数的小数展开形式。解答：（i）$\frac{13}{3125}=\frac{13}{5^5}$将分子和分母乘以 $2^5$，使分母成为 $10^r$ 的倍数，其中 r 是任何正整数。因此，$\frac{13}{3125}=\frac{13}{5^5}$$=\frac{13\times2^5}{5^5\times2^5}$$=\frac{13\times32}{(2\times5)^5}$$=\frac{416}{10^5}$$=\frac{416}{100000}$$=0.00416$给定有理数的小数展开形式为 $0.00416$。（ii）$\frac{17}{8}=\frac{17}{2^3}$将分子和分母乘以 $5^3$，使分母成为 $10^r$ 的倍数，其中 r 是任何正整数。因此，$\frac{17}{8}=\frac{17}{2^3}$$=\frac{17\times5^3}{2^3\times5^3}$$=\frac{17\times125}{(2\times5)^3}$$=\frac{2125}{10^3}$$=\frac{2125}{1000}$$=2.125$给定有理数的小数展开形式为 $2.125$。（iii）$\frac{15}{1600}=\frac{15}{2^6\times5^2}$将分子和分母乘以 $5^4$，使分母成为 $10^r$ 的倍数，其中 r 是 ... 阅读更多
要做的：这里，我们需要确定当给定有理数表示为 $\frac{p}{q}$ 形式时，其分母的素因数分解的性质。解答：（i）$43.123456789$ 具有有限小数展开形式。这意味着它是有理数，形式为 $\frac{p}{q}$，并且 $q$ 的形式为 $2^m \times 5^n$，其中 $p$ 和 $q$ 是非负整数。给定有理数的分母的素因子为 $2$ 和 $5$。（ii）$0.120120012000120000$.... 具有无限不循环小数展开形式。给定有理数的分母具有除 $2$ 或 $5$ 之外的其他因子。因此，给定的实数不是有理数。（iii）$43.\overline{123456789}$ 具有 ... 阅读更多
"
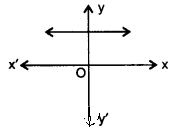
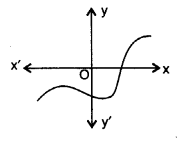
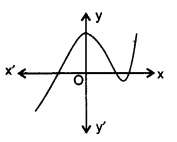
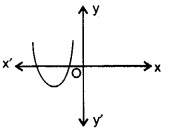
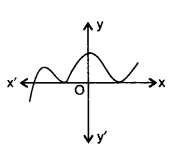
要做的：我们需要在每种情况下求出 $p(x)$ 的零点个数。解答：（i）给定的图形在任何点都不与 x 轴相交。因此，零点个数为 $0$。（ii）图形在一点与 x 轴相交。因此，零点个数为 $1$。（iii）图形在三点与 x 轴相交。因此，零点个数为 $3$。（iv）图形在两点与 x 轴相交。因此，零点个数为 $2$。（v）图形在 $4$ 个点与 x 轴相交。因此，零点个数为 $4$。（vi）图形在 $3$ 个点与 x 轴相交。 ... 阅读更多
要做的：我们需要将给定的代数表达式相加。解答：（i）$3 a^{2} b+(-4 a^{2} b)+9 a^{2} b=a^{2} b(3-4+9)$$=8 a^{2} b$(ii) $\frac{2}{3} a+\frac{3}{5} a+(\frac{-6}{5} a)=(\frac{2}{3}+\frac{3}{5}-\frac{6}{5}) a$$=\frac{10+9-18}{15} a$ (3 和 5 的最小公倍数是 15)$=\frac{19-18}{15} a$$=\frac{1}{15} a$(iii) $4 x y^{2}-7 x^{2} y+12 x^{2} y-6 x y^{2}-3 x^{2} y+5 x y^{2}=4 x y^{2}-6 x y^{2}+5 x y^{2}-7 x^{2} y+12 x^{2} y-3 x^{2} y$$=(4-6+5) x y^{2}+(-7+12-3) x^{2} y$$=3 x y^{2}+2 x^{2} y$(iv) $\frac{3}{2} a-\frac{5}{4} b+\frac{2}{5} c+\frac{2}{3} a-\frac{7}{2} b+\frac{7}{2} c+\frac{5}{3} a+\frac{5}{2} b-\frac{5}{4} c=\frac{3}{2} a+\frac{2}{3} a+\frac{5}{3} a-\frac{5}{4} b-\frac{7}{2} b+\frac{5}{2} b+\frac{2}{5} c+\frac{7}{2} c-\frac{5}{4} c$$=(\frac{9 a+4 a+10 a}{6})+(\frac{-5 b-14 b+10 b}{4})+(\frac{8 c+70 c-25 c}{20})$$=\frac{23}{6} a-\frac{9}{4} b+\frac{53}{20} ... 阅读更多
要做的：我们需要减去给定的代数表达式。解答：（i）$12 x y-(-5 x y)=12 x y+5 x y$$=17 x y$(ii) $-7 a^{2}-2 a^{2}=(-7-2)a^2$$=-9 a^{2}$ (iii) $(3 a-5 b)-(2 a-b)=3 a-5 b-2 a+b$$=3 a-2 a-5 b+b$$=a-4 b$(iv) $(4 x^{3}+x^{2}+x+6)-(2 x^{3}-4 x^{2}+3 x+5)=4 x^{3}+x^{2}+x+6-2 x^{3}+4 x^{2}-3 x-5$$=4 x^{3}-2 x^{3}+x^{2}+4 x^{2}+x-3 x+6-5$$=2 x^{3}+5 x^{2}-2 x+1$(v) $(\frac{1}{3} y^{3}+\frac{5}{7} y^{2}+y-2)-(\frac{2}{3} y^{3}-\frac{2}{7} y^{2}-5)$$=\frac{1}{3} y^{3}+\frac{5}{7} y^{2}+y-2-\frac{2}{3} y^{3}+\frac{2}{7} y^{2}+5$$=\frac{1}{3} y^{3}-\frac{2}{3} y^{3}+\frac{5}{7} y^{2}+\frac{2}{7} y^{2}+y-2+5$$=\frac{1-2}{3} y^{3}+\frac{5+2}{7} y^{2}+y+3$$=\frac{-1}{3} y^{3}+\frac{7}{7} y^{2}+y+3$$=\frac{-1}{3} y^{3}+y^{2}+y+3$(vi) $(\frac{2}{3} x+\frac{3}{2} y-\frac{4}{3} z)-(\frac{3}{2} x-\frac{5}{4} y-\frac{7}{2} z)=\frac{2}{3} x+\frac{3}{2} y-\frac{4}{3} z-\frac{3}{2} x+\frac{5}{4} y+\frac{7}{2} z$$=\frac{2}{3} x-\frac{3}{2} x+\frac{3}{2} y+\frac{5}{4} y-\frac{4}{3} z+\frac{7}{2} z$$=\frac{4-9}{6} x+\frac{6+5}{4} y+\frac{-8+21}{6} z$$=\frac{-5}{6} x+\frac{11}{4} y+\frac{13}{6} z$(vii) $(\frac{2}{3} x^{2} y+\frac{3}{2} x y^{2}-\frac{1}{3} x ... 阅读更多
解题思路：我们需要将给定的代数表达式减去。解答：(i) $(\frac{x^{3}}{3}-\frac{5}{2} x^{2}+\frac{3}{5} x+\frac{1}{4})-(\frac{6}{5} x^{2}-\frac{4}{5} x^{3}+\frac{5}{6}+\frac{3}{2} x)=\frac{x^{3}}{3}-\frac{5}{2} x^{2}+\frac{3}{5} x+\frac{1}{4}-\frac{6}{5} x^{2}+\frac{4}{5} x^{3}-\frac{5}{6}-\frac{3}{2} x$$=\frac{x^{3}}{3}+\frac{4}{5} x^{3}-\frac{5}{2} x^{2}-\frac{6}{5} x^{2}+\frac{3}{5} x-\frac{3}{2} x+\frac{1}{4}-\frac{5}{6}$$=(\frac{1}{3}+\frac{4}{5}) x^{3}+(\frac{-5}{2}-\frac{6}{5}) x^{2}+(\frac{3}{5}-\frac{3}{2}) x+(\frac{1}{4}-\frac{5}{6})$$=\frac{5+12}{15} x^{3}+\frac{-25-12}{10} x^{2}+\frac{6-15}{10} x+\frac{3-10}{12}$$=\frac{17}{15} x^{3}-\frac{37}{10} x^{2}-\frac{9}{10} x-\frac{7}{12}$(ii) $(\frac{1}{3} a^{3}-\frac{3}{4} a^{2}-\frac{5}{2})-(\frac{5 a^{2}}{2}+\frac{3 a^{3}}{2}+\frac{a}{3}-\frac{6}{5})=\frac{1}{3} a^{3}-\frac{3}{4} a^{2}-\frac{5}{2}-\frac{5}{2} a^{2}-\frac{3}{2} a^{3}-\frac{a}{3}+\frac{6}{5}$$=\frac{1}{3} a^{3}-\frac{3}{2} a^{3}-\frac{3}{4} a^{2}-\frac{5}{2} a^{2}-\frac{a}{3}+\frac{6}{5}-\frac{5}{2}$$=(\frac{1}{3}-\frac{3}{2}) a^{3}-(\frac{3}{4}+\frac{5}{2}) a^{2}-(\frac{1}{3}) a+(\frac{6}{5}-\frac{5}{2})$$=\frac{2-9}{6} a^{3}-\frac{3+10}{4} a^{2}-\frac{1}{3} a+\frac{12-25}{10}$$=\frac{-7}{6} a^{3}-\frac{13}{4} a^{2}-\frac{1}{3} a-\frac{13}{10}$(iii) $(\frac{7}{2}-\frac{x}{3}-\frac{x^{2}}{5})-(\frac{7}{4} x^{3}+\frac{3}{5} x^{2}+\frac{1}{2} x+\frac{9}{2})=\frac{7}{2}-\frac{x}{3}-\frac{x^{2}}{5}-\frac{7}{4} x^{3}-\frac{3}{5} x^{2}-\frac{1}{2} x-\frac{9}{2}$$=\frac{-7}{4} x^{3}-\frac{x^{2}}{5}-\frac{3}{5} x^{2}-\frac{x}{3}-\frac{1}{2} x+\frac{7}{2}-\frac{9}{2}$$=\frac{-7}{4} x^{3}-(\frac{1}{5}+\frac{3}{5}) x^{2}-(\frac{1}{3}+\frac{1}{2}) x+\frac{7-9}{2}$$=\frac{-7}{4} x^{3}-\frac{1+3}{5} x^{2}-\frac{2+3}{6} x-\frac{2}{2}$$=\frac{-7}{4} x^{3}-\frac{4}{5} x^{2}-\frac{5}{6} x-1$(iv) $(\frac{1}{3}-\frac{5}{3} y^{2})-(\frac{y^{3}}{3}+\frac{7}{3} y^{2}+\frac{1}{2} y+\frac{1}{2})=\frac{1}{3}-\frac{5}{3} y^{2}-\frac{y^{3}}{3}-\frac{7}{3} y^{2}-\frac{1}{2} y-\frac{1}{2}$$=\frac{-y^{3}}{3}-(\frac{5}{3}+\frac{7}{3}) y^{2}-\frac{1}{2} y-\frac{1}{2}+\frac{1}{3}$$=\frac{-y^{3}}{3}-\frac{5+7}{3} y^{2}-\frac{1}{2} y-\frac{3-2}{6}$$=\frac{-y^{3}}{3}-\frac{12}{3} y^{2}-\frac{1}{2} y-\frac{1}{6}$$=\frac{-1}{3} y^{3}-4 y^{2}-\frac{1}{2} y-\frac{1}{6}$(v) $(\frac{3}{2} a b-\frac{7}{4} a c-\frac{5}{6} b c)-(\frac{2}{3} ... 阅读更多
解题思路：我们需要从 $x - 3y + 2z$ 和 $-4x + 9y- 11z$ 的和中减去 $3x - 4y - 7z$。解答：$x - 3y + 2z$ 和 $-4x + 9y - 11z$ 的和为，$x - 3y + 2z + (- 4x + 9y - 11z) = x - 3y + 2z - 4x + 9y - 11z$$= x - 4x - 3y + 9y + 2z - 11z$$= -3x + 6y - 9z$从 $(-3x + 6y - 9z)$ 中减去 $3x - 4y - 7z$ $(-3x + 6y - 9z)-(3x - 4y - 7z)=-3x + 6y - 9z ... 阅读更多
解题思路：我们需要从 $9l + 2m - 3n^2$ 和 $-3l + m + 4n^2$ 的和中减去 $3l- 4m - 7n^2$ 和 $2l + 3m - 4n^2$ 的和。解答：$9l + 2m - 3n^2$ 和 $-3l + m + 4n^2$ 的和为，$9l + 2m - 3n^2 + (-3l + m + 4n^2)= 9l + 2m - 3n^2 - 3l + m + 4n^2$$= 9l- 3l+ 2m + m - 3 n^2 + 4n^2$$= 6l + 3m + n^2$ $3l - 4m - 7n^2$ 和 $2l +3m- 4n^2$ 的和为，$3l- 4m - 7n^2 +(2l+ ... 阅读更多
解题思路：我们需要从 5 中减去 $2x - x^2 + 5$ 和 $-4x - 3 + 7x^2$ 的和。解答：$2x - x^2 + 5$ 和 $-4x - 3 + 7x^2$ 的和为，$2x - x^2 + 5+(-4x - 3 + 7x^2)=2x - 4x- x^2 + 7x^2 + 5-3$$=-2x+6x^2+2$从 5 中减去 $-2x+6x^2+2$，$5-(-2x+6x^2+2)=5+2x-6x^2-2$$=-6x^2+2x+3$
解题思路：我们需要解出给定的表达式。解答：(i) $x^{2}-3 x+5-\frac{1}{2}(3 x^{2}-5 x+7) =x^{2}-3 x+5-\frac{3}{2} x^{2}+\frac{5}{2} x-\frac{7}{2}$$=x^{2}-\frac{3}{2} x^{2}-3 x+\frac{5}{2} x+5-\frac{7}{2}$$=(1-\frac{3}{2}) x^{2}-(3-\frac{5}{2}) x+(\frac{5}{1}-\frac{7}{2})$$=\frac{2-3}{2} x^{2}-\frac{6-5}{2} x+\frac{10-7}{2}$$=\frac{-1}{2} x^{2}-\frac{1}{2} x+\frac{3}{2}$(ii) $[5-3 x+2 y-(2 x-y)]-(3 x-7 y+9)=[5-3 x+2 y-2 x+y]-(3 x-7 y+9)$$=5-3 x+2 y-2 x+y-3 x+7 y-9$$=5-9-3 x-2 x-3 x+2 y+y+7 y$ $=-4-8 x+10 y$(iii) $\frac{11}{2} x^{2} y-\frac{9}{4} x y^{2}+\frac{1}{4} x y-\frac{1}{14} y^{2} x+\frac{1}{15} y x^{2}+\frac{1}{2} x y=\frac{11}{2} x^{2} y+\frac{1}{15} y x^{2}-\frac{9}{4} x y^{2}-\frac{1}{14} y^{2} x+\frac{1}{4} x y+\frac{1}{2} x y$$=(\frac{165+2}{30}) x^{2} y+(\frac{-63-2}{28}) x y^{2}+(\frac{1+2}{4}) x y$$=\frac{167}{30} x^{2} y-\frac{65}{28} y^{2} x+\frac{3}{2} x y$(iv) $(\frac{1}{3} y^{2}-\frac{4}{7} y+11)-(\frac{1}{7} y-3+2 y^{2})-(\frac{2}{7} y-\frac{2}{3} y^{2}+2)=\frac{1}{3} y^{2}-\frac{4}{7} y+11-\frac{1}{7} y+3-2 y^{2}-\frac{2}{7} y+\frac{2}{3} y^{2}-2$$=\frac{1}{3} ... 阅读更多