数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学
"\
已知：$ABCD$是一个圆内接四边形，$AC$和$BD$是它的对角线。$\angle DBC = 55^o$且$\angle BAC = 45^o$。求解：我们需要求$\angle BCD$。解：$\angle BAC$和$\angle BDC$在同一段圆弧上。这意味着，$\angle BAC = \angle BDC = 45^o$在$\triangle BCD$中，$\angle DBC + \angle BDC + \angle BCD = 180^o$ (三角形的内角和)$55^o + 45^o + \angle BCD = 180^o$$100^o + \angle BCD = 180^o$$\angle BCD = 180^o - 100^o = 80^o$因此 $\angle BCD = 80^o$。
已知：以三角形的各边为直径作圆。求解：我们需要证明任意两边上的圆在第三边（或第三边的延长线上）相交。解：设在$\triangle ABC$中，以边$AB$和$AC$为直径作圆。作$AD \perp BC$ $AD \perp BC$这意味着，$\angle ADB = \angle ADC = 90^o$从图中可以看出，以$AB$和$AC$为直径作的圆将经过$D$点。因此，以三角形的两边为直径作的圆经过$D$点，而$D$点位于第三边上。 阅读更多
已知：圆内接四边形的一对对边的两边相等。求解：我们需要证明它的对角线相等。解：设在圆内接四边形$ABCD$中，$AB = CD$，$AC$和$BD$是对角线。$AB = CD$弧$AB =$ 弧$CD$在两边都加上弧$BC$，得到：弧$AB +$ 弧$BC =$ 弧$BC +$ 弧$CD$弧$AC =$ 弧$BD$因此，$AC = BD$因此，圆内接四边形的对角线相等。
已知：$ABCD$是一个圆内接四边形，其中$\angle BCD = 100^o$且$\angle ABD = 70^o$。求解：我们需要求$\angle ADB$。解：$ABCD$是一个圆内接四边形。连接$BD$。$\angle BCD = 100^o$且$\angle ABD = 70^o$$\angle A + \angle C = 180^o$ (圆内接四边形的对角互补)$\angle A+ 100^o = 180^o$$\angle A= 180^o - 100^o$$\angle A = 80^o$在$\triangle ABD$中，$\angle A + \angle ABD + \angle ADB = 180^o$ (三角形的内角和)$80^o + 70^o + \angle ADB = 180^o$$150^o +\angle ADB = 180^o$$\angle ADB = 180^o- 150^o$$= 30^o$因此 $\angle ADB = 30^o$。
求解：我们需要证明以菱形的四条边为直径所作的圆都经过其对角线的交点。解：设$ABCD$是一个菱形。分别以边$AB, BC, CD$和$DA$为直径作四个圆。$ABCD$是一个菱形，其对角线$AC$和$BD$相交于$O$点。菱形的对角线互相垂直平分。这意味着，$\angle AOB = \angle BOC = \angle COD = \angle DOA = 90^o$$\angle AOB = 90^o$，以$AB$为直径作的圆将经过$O$点。类似地，以$BC,... 阅读更多
已知：$ABCD$是一个圆内接四边形，其中$BC \| AD$，$\angle ADC =110^o$且$\angle BAC = 50^o$。求解：我们需要求$\angle DAC$。解：$ABCD$是一个圆内接四边形。这意味着，$\angle B + \angle D = 180^o$ (圆内接四边形的对角互补)$\angle B + 110^o = 180^o$$\angle B = 180^o - 110^o = 70^o$在$\triangle ABC$中，$\angle CAB + \angle ABC + \angle BCA = 180^o$ (三角形的内角和)$50^o + 70^o + \angle BCA = 180^o$$120^o + \angle BCA = 180^o$$\angle BCA = 180^o - 120^o$$= 60^o$$\angle DAC = \angle BCA$ (内错角相等)$\angle DAC = 60^o$因此 $\angle DAC = 60^o$。
已知：$ABCD$是一个圆内接四边形，其中$\angle DBC = 80^o$且$\angle BAC = 40^o$。求解：我们需要求$\angle BCD$。解：$ABCD$是一个圆内接四边形。连接对角线$AC$和$BD$。$\angle DBC = 80^o, \angle BAC = 40^o$弧$DC$在同一段圆弧上对角$\angle DBC$和$\angle DAC$因此，$\angle DBC = \angle DAC = 80^o$$\angle DAB = \angle DAC + \angle CAB$$= 80^o + 40^o$$= 120^o$$\angle DAC + \angle BCD = 180^o$ (圆内接四边形的对角互补)$120^o +\angle BCD = 180^o$$\angle BCD = 180^o- 120^o$$= 60^o$因此 $\angle BCD = 60^o$。
已知：在圆内接四边形$ABCD$中，$\angle A - \angle C = 60^o$求解：我们需要证明较小的角是$60^o$。解：$\angle A - \angle C = 60^o$...........(i)$ABCD$是一个圆内接四边形。这意味着，$\angle A + \angle C = 180^o$...........(ii) (圆内接四边形的对角互补)将(i)和(ii)相加，得到：$2\angle A = 240^o$$\angle A = 120^o$将$\angle A = 120^o$代入(i)，得到：$120^o-\angle C = 60^o$$\angle C = 120^o-60^o$$\angle C = 60^o$因此，这两个角中较小的角是$60^o$。
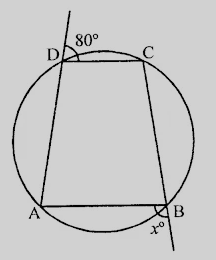
"\已知：$ABCD$是一个圆内接四边形。求解：我们需要求$x$的值。解：$\angle CDE + \angle CDA = 180^o$ (邻补角) $80^o + \angle CDA = 180^o$$\angle CDA = 180^o - 80^o$$= 100^o$在圆内接四边形$ABCD$中，外角$\angle B = $内对角$\angle CDA$$= 100^o$因此，$x = 100^o$$x$的值为$100^o$。
"\已知：$\angle BAD = 78^o, \angle DCF = x^o$且$\angle DEF = y^o$。求解：我们需要求$x$和$y$的值。解：在给定的图中，两个圆相交于$C$和$D$点。$\angle BAD = 78^o, \angle DCF = x, \angle DEF = y$$ABCD$是一个圆内接四边形。$\angle DCF = $内对角$\angle BAD$$x = 78^o$在圆内接四边形$CDEF$中，$\angle DCF + \angle DEF = 180^o$$78^o + y = 180^o$$y = 180^o - 78^o$$y = 102^o$因此 $x = 78^o$且$y = 102^o$。