数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
已知：一个实心木制玩具，形状为半球体上有一个与半球体半径相同的圆锥体。半球体的半径为 \( 3.5 \mathrm{~cm} \)，制作玩具所用木材的总量为 \( 166 \frac{5}{6} \mathrm{~cm}^{3} \)。 需要求解：我们需要找到玩具的高度以及以 \( ₹ 10 \) 每 \( \mathrm{cm}^{2} \) 的价格涂刷玩具半球体部分的费用。 解答：制作玩具所用木材的体积 $=166 \frac{5}{6} \mathrm{~cm}^{3}$$=\frac{1001}{6} \mathrm{~cm}^{3}$半球体的半径 $=3.5 \mathrm{~cm}$设 $h$ 为圆锥体的高度 ... 阅读更多
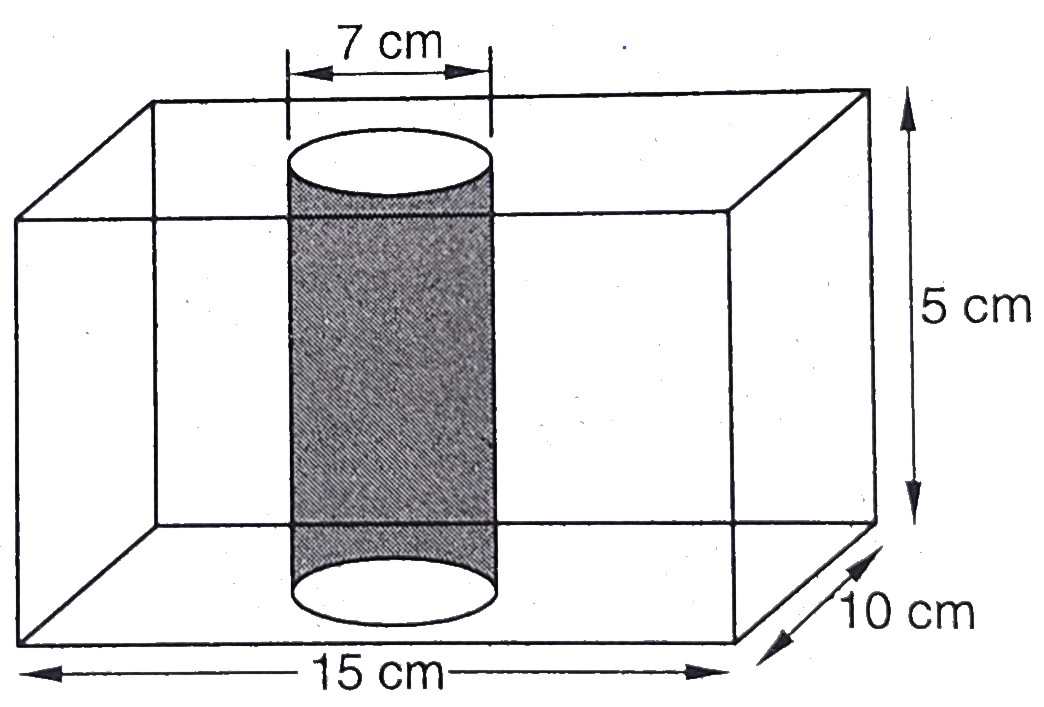
"\已知：从一个长方体实心金属块中（尺寸为 \( 15 \mathrm{~cm} \times 10 \mathrm{~cm} \) \( \times 5 \mathrm{~cm} \)），钻出一个直径为 \( 7 \mathrm{~cm} \) 的圆柱形孔。需要求解：我们需要找到剩余块体的表面积。解答：长方体实心金属块的尺寸为 $15\ cm \times\ 10\ cm \times 5\ cm$孔的半径 $= \frac{7}{2}\ cm$圆柱体的高度 $= 5\ cm$块体的长度 $l = 15\ cm$块体的宽度 $b = 10\ cm$块体的高度 $h= 5\ cm$因此，块体的表面积 $= 2(lb + bh + ... 阅读更多
已知：一块宽 \( 5 \mathrm{~m} \) 的布料用来制作一个圆锥形帐篷，帐篷底面直径为 \( 14 \mathrm{~m} \)，高 \( 24 \mathrm{~m} \)。需要求解：我们需要找到以 \( ₹ 25 \) 每米的价格计算所用布料的费用。解答：圆锥形帐篷底面直径 $= 14\ m$这意味着，底面半径 $r= \frac{14}{2}$$=7\ m$圆锥体的高度 $h = 24\ m$这意味着，圆锥体的斜高 $l=\sqrt{r^{2}+h^{2}}$$=\sqrt{7^{2}+24^{2}}$$=\sqrt{49+576}$$=\sqrt{625}$$=25 \mathrm{~m}$因此，圆锥体的侧面积 $=\pi r l$$=\frac{22}{7} \times 7 \times 25$$=550 \mathrm{~m}^{2}$所用布料的宽度 $=5 \mathrm{~m}$这意味着， ... 阅读更多
已知：一个半球体的体积为 \( 2425 \frac{1}{2} \mathrm{~cm}^{3} \)。需要求解：我们需要找到其曲面面积。解答：半球体的体积 $=2425 \frac{1}{2} \mathrm{~cm}^{3}$$=\frac{4851}{2} \mathrm{~cm}^{3}$设 $r$ 为半球体的半径。因此，半球体的体积 $=\frac{1}{2} \times \frac{4}{3} \pi r^{3}$$\Rightarrow \frac{2}{3} \times \frac{22}{7} r^{3}=\frac{4851}{2}$$\Rightarrow r^{3}=\frac{4851}{2} \times \frac{3 \times 7}{2 \times 22}$$\Rightarrow r^{3}=\frac{441 \times 21}{2 \times 2 \times 2}$$\Rightarrow r^{3}=\frac{21 \times 21 \times 21}{2 \times 2 \times 2}$$\Rightarrow r^{3}=(\frac{21}{2})^{3}$$\Rightarrow r=\frac{21}{2} \mathrm{~cm}$半球体的曲面面积 $=2 \pi r^{2}$$=2 \times \frac{22}{7} \times(\frac{21}{2})^{2}$$=\frac{2 \times 22 \times 21 \times 21}{7 \times 2 \times 2}$$=693 \mathrm{~cm}^{2}$半球体的曲面面积 ... 阅读更多
已知：一个空心直圆柱体长 \( 14 \mathrm{~cm} \)，其内外曲面面积之差为 \( 88 \mathrm{~cm}^{2} \)。制作圆柱体所用金属的体积为 \( 176 \mathrm{~cm}^{3} \)。需要求解：我们需要找到圆柱体的内外直径。解答：空心直圆柱体的高度 $= 14\ cm$内外曲面面积之差 $= 88\ cm^2$制作圆柱体所用金属的体积 $=176\ cm^3$设 $\mathrm{R}$ 和 $r$ 为圆柱体的内外半径。$\Rightarrow \pi R^{2} h-\pi r^{2} h=176$$\Rightarrow \pi ... 阅读更多
已知：一个空心半球形容器的内外直径分别为 \( 21 \mathrm{~cm} \) 和 \( 25.2 \mathrm{~cm} \)。涂刷表面积 \( 1 \mathrm{~cm}^{2} \) 的费用为 10 分。需要求解：我们需要找到涂刷整个容器所需的总费用。解答：空心半球形容器的外直径 $= 25.2\ cm$空心半球形容器的内直径 $= 21\ cm$这意味着，外半径 $\mathrm{R}=\frac{25.2}{2}$$=12.6 \mathrm{~cm}$内半径 $r=\frac{21}{2}$$=10.5 \mathrm{~cm}$容器的总表面积 $=$ 外表面积 $+$ 内表面积 $+$ 底面积$=2 \pi \mathrm{R}^{2}+2 \pi r^{2}+(\pi \mathrm{R}^{2}-\pi r^{2})$$=2 \pi \mathrm{R}^{2}+2 \pi ... 阅读更多
待解决问题：我们需要证明球的表面积等于其外接圆柱的侧面积。解答：设球的半径为r。这意味着，球的表面积 = 4πr²。……(i)球的直径 = 圆柱的高h = 2r外接圆柱的半径 = 球的半径 = r因此，圆柱的侧面积 = 2πrh = 2πr × 2r = 4πr².........(ii)由公式 (i) 和 (ii) 可知，球的表面积 = 外接圆柱的侧面积因此得证。阅读更多
已知：实心半球的总表面积为\( 462 \mathrm{~cm}^{2} \)。待解决问题：我们需要求出实心半球的体积。解答：实心半球的总表面积 = 462 cm²设半球的半径为r。因此，圆柱的总表面积 = 3πr²3πr² = 462⇒ \frac{3 \times 22}{7} r^{2}=462⇒ r² = \frac{462 \times 7}{3 \times 22}⇒ r² = 49⇒ r² = (7)²⇒ r = 7 cm实心半球的体积 = \frac{2}{3} πr³ = \frac{2}{3} × \frac{22}{7} × 7³ = \frac{2156}{3} = 718 \frac{2}{3} cm³实心半球的体积为 718 \frac{2}{3} cm³。
已知：水以每分钟 10 米的速度流过直径为 5 毫米的圆柱形管道。圆锥形容器的直径 = 40 厘米圆锥形容器的深度 = 24 厘米。待解决问题：我们需要求出灌满圆锥形容器所需的时间。解答：水的流速 = 10 米/分钟 = 1000 厘米/分钟圆柱形管道的半径 = \frac{5}{10 \times 2} = 0.25 厘米这意味着，管道的截面积 = πr² = \frac{22}{7} × (0.25)² = 0.1964 cm²圆锥形容器的半径 R = \frac{40}{2} = 20 厘米圆锥形容器的深度 H = 24 厘米因此，圆锥形容器的体积 = \frac{1}{3} πR²H = \frac{1}{3} × \frac{22}{7} × (20)² × 24 = \frac{211200}{21} = 10057.14 cm³灌满所需的时间 ... 阅读更多
已知：一个高 120 厘米，半径 60 厘米的实心直圆锥体放入一个装满水的直圆柱体中，圆柱体高 180 厘米，且圆锥体底面与圆柱体底面接触。圆柱体的半径等于圆锥体的半径。待解决问题：我们需要求出圆柱体中剩余水的体积。解答：直圆锥体的高 h = 120 厘米圆锥体的半径 r = 60 厘米直圆柱体的高 H = 180 厘米圆柱体的半径 R = 60 厘米圆柱体中剩余水的体积 = 圆柱体的体积 - 圆锥体的体积 = πr²h - \frac{1}{3} ... 阅读更多