数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法学
已知：圆的半径 $r=6 \mathrm{~cm}$。弧长 $l=10 \mathrm{~cm}$。圆心角 $=110^{\circ}$。求解：我们需要求圆的面积。解：设 $OA$ 和 $OB$ 是圆的半径，$AB$ 是弦。我们知道，半径为 $r$ 的圆的面积是 $\pi r^2$。因此，圆的面积 $=3.14 \times 6 \times 6\ cm$$=113.04\ cm^2$ 圆的面积是 $113.04\ cm^2$。
已知：圆的半径 $r=6 \mathrm{~cm}$。弧长 $l=10 \mathrm{~cm}$。圆心角 $=110^{\circ}$。求解：我们需要求弧 \( AB \) 的长度。解：设 $OA$ 和 $OB$ 是圆的半径，$AB$ 是弦。我们知道，在圆心处构成 $\theta$ 角的弧长是 $2 \pi r (\frac{\theta}{360^{\circ}})$。因此，弧长 $=2 \pi r \times \frac{\theta}{360^{\circ}}$$=2 \times 3.14 \times 6 \times \frac{110^{\circ}}{360^{\circ}} \mathrm{cm}$$=12 \times 3.14 \times \frac{11}{36} \mathrm{cm}$$=\frac{34.54}{3} \mathrm{cm}$$=11.51 \mathrm{~cm}$ 弧长是 $11.51\ cm$。 阅读更多
已知：圆的半径 $r=6 \mathrm{~cm}$。弧长 $l=10 \mathrm{~cm}$。圆心角 $=110^{\circ}$。求解：我们需要求扇形 \( OAB \) 的面积。解：设 $OA$ 和 $OB$ 是圆的半径，$AB$ 是弦。我们知道，扇形的面积是 $\pi r^{2} (\frac{\theta}{360^{\circ}})$。因此，扇形 $OAB$ 的面积 $=\pi r^{2} \times \frac{\theta}{360^{\circ}}$$= 3.14 \times 6 \times 6 \times \frac{110^{\circ}}{360^{\circ}} \mathrm{cm}^{2}$$=36 \times 3.14 \times \frac{11}{36} \mathrm{~cm}^{2}$$=34.54 \mathrm{~cm}^{2}$ 扇形 \( OAB \) 的面积是 $34.54\ cm^2$。 阅读更多
已知： $\frac{a^{2n+1} \times a^{(2n+1)(2n-1)}}{a^{n(4n-1)}\times(a^{2})^{2n+3}}$。求解： $\frac{a^{2n+1}\times a^{(2n+1)(2n-1)}}{a^{n(4n-1)}\times(a^{2})^{2n+3}}$。解： $\frac{a^{2n+1}\times a^{(2n+1)(2n-1)}}{a^{n(4n-1)}\times(a^{2})^{2n+3}}$$=\frac{a^{( 2n+1)} \times a^{( 4n^2-1)}}{a^{(4n^2-n)}\times a^{( 4n+6)}}$$=\frac{a^{( 2n+1+4n^2-1)}}{a^{( 4n^2-n+4n+6)}}$$=a^{( 2n+1+4n^2-1-4n^2+n-4n-6)}$$=a^{( -n-6)}$$=a^{-( n+6)}$$=\frac{1}{a^{( n+6)}}$$=\frac{1}{a^n\times a^{6}}$
我们知道导体的电阻和导体的长度成正比 $(L \propto R)$，这意味着随着导体长度的增加，导体的电阻也增加。而如果长度减小，则电阻也减小。类似地，导体的横截面积和电阻成反比 $(A\propto \frac {1}{R})$，这意味着随着横截面积的增加，电阻减小。而如果横截面积减小，则电阻增加。已知：电阻，$R$ = $10\Omega$ 求解：电阻 ... 阅读更多
已知：A 是 B 的 50%。求解：B 是 (A+B) 的百分之几？解：如已知，A 是 B 的 50%。$\Rightarrow A=\frac{B}{100}\times 50$$\Rightarrow A=\frac{B}{2}$因此，$A+B=\frac{B}{2}+B=\frac{3B}{2}$设 B 是 (A+B) 的 x%。$\Rightarrow B=\frac{3B}{2}\times\frac{x}{100}$$\Rightarrow 1=\frac{3x}{200}$$\Rightarrow 3x=200$$\Rightarrow x=\frac{200}{3}=66\frac{2}{3}$因此，B 是 (A+B) 的 $66\frac{2}{3}$ %。所以，(B) 正确。
已知：一个农民有一个等腰梯形形状的田地，周长为 $215\ m$。其中一条不平行的边长为 $50\ m$。求解：求其平行边的和。解：如已知，等腰梯形田地的周长 $=215\ m$ 一条不平行边的长度 $=50\ m$ 第二条不平行边的长度 $=50\ m$ [等腰梯形的性质] $(不平行边之和)+(平行边之和)=215$ $\Rightarrow ( 50 + 50)+( 平行边之和)=215$ $\Rightarrow$ 平行边的和 $=215-100=115\ m$ 因此，其平行边的和是 $115\ m$。
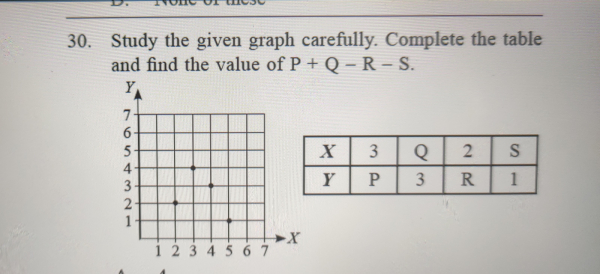
"\求解：需要完成给定的表格并求 $P+Q-R-S$ 的值。解：在给定的图表中，我们得到：当 $X=3\Rightarrow Y=4\Rightarrow P=4$当 $Y=3\Rightarrow X=4\Rightarrow Q=4$当 $X=2\Rightarrow Y=2\Rightarrow R=2$当 $Y=1\Rightarrow X=5\Rightarrow S=5$完整的表格如下所示：$X$$3$$Q=4$$2$$S=5$$Y$$P=4$$3$$R=2$$1$ 现在，$P+Q-R-S=4+4-2-5=8-7=1$。
求解：我们需要证明围绕半径为 $r$ 的圆形区域的宽度为 $h$ 的均匀圆形路径的面积是 $\pi h(2r + h)$。解：内圆半径 $= r$ 路径宽度 $= h$这意味着，外半径 $R = r + h$因此，路径面积 $= \pi R^2 - \pi r^2$$= \pi [(r + h)^2 - r^2]$$= \pi (r^2 + h^2 + 2rh – r^2)$$= \pi (2rh + h^2)$$= \pi h (2r + h)$ 证毕。
已知：圆弧在半径为 4 厘米的圆的圆心处张成一个 30° 的角。求：求圆弧的长度（用 π 表示）。解：圆的半径 r = 4 cm圆心角 = 30°我们知道，在圆心处张成 θ 角的圆弧长度 = 2πr(θ/360°)因此，圆弧长度 = 2 × 4 × π × (30°/360°) = 8π × (1/12) = (2/3)π cm圆弧长度为 (2/3)π cm。