数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
已知: $( a).$ VV $( b).$ ID $( c).$ VC $( d).$ XXXX 解题步骤：证明给定的罗马数字无意义。解答: $( a).$ VV 已知 V 不能相减，因此 VV 无意义。 $( b).$ ID 已知 I 只能从 V 和 X 中减去。因此 ID 无意义。 $( c).$ VC V 不能相减。因此 VC 无意义。 $( d).$ XXXX 无意义，因为任何符号都不能重复超过 3 次。
已知：表达式：$\frac{2m+5}{3}=3m-10$。解题步骤：解方程 $\frac{2m+5}{3}=3m-10$。解答：已知表达式：$\frac{2m+5}{3}=3m-10$ $\Rightarrow 2m+5=3( 3m-10)$ $\Rightarrow 2m+5=9m-30$ $\Rightarrow 9m-2m=30+5$ $\Rightarrow 7m=35$ $\Rightarrow m=\frac{35}{7}$ $\Rightarrow m=5$
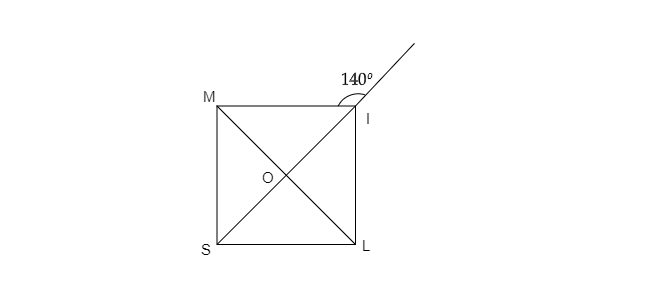
"\已知：如图所示，SLIM 是一个矩形。解题步骤：求 $\angle SOL$。解答：在 $\vartriangle MOI$ 中，$\angle MIO=180^o-140^o=40^o$ $\because ML=SI$ [对角线 SI 和 ML 相等且互相平分] $\therefore \angle OMI=\angle MIO=40^o$ $\Rightarrow \angle OMI+\angle MIO+\angle MOI=180^o$ $\Rightarrow 40^o+40^o+\angle MOI=180^o$ $\Rightarrow 80^o+\angle MOI=180^o$ $\Rightarrow \angle MOI=180^o-80^o$ $\Rightarrow \angle MOI=100^o$ 因此，$\angle SOL=\angle MOI=100^o$。
已知：一根旗杆立在5米高的塔顶上。从地面上的一点，测得旗杆顶端的仰角为\( 60^{\circ} \)，从同一点测得塔顶的仰角为\( 45^{\circ} \)。解题步骤：我们必须找到旗杆的高度。解答：设 AB 为塔，BC 为旗杆的长度。设 D 为观察点。从图中，$\mathrm{AB}=5 \mathrm{~m}, \angle \mathrm{CDA}=60^{\circ}, \angle \mathrm{BDA}=45^{\circ}$设旗杆的高度为 $\mathrm{BC}=h \mathrm{~m}$，塔与…… 阅读更多
已知：从一座 50 米高的塔顶，观察到一根杆子的顶部和底部的俯角分别为 \( 45^{\circ} \) 和 \( 60^{\circ} \)。解题步骤：我们必须找到杆子的高度。解答：设 AB 为塔，CD 为杆子。设 B 为观察点。从图中，$\mathrm{AB}=50 \mathrm{~m}, \angle \mathrm{BDE}=45^{\circ}, \angle \mathrm{BCA}=60^{\circ}$设杆子的高度为 $\mathrm{CD}=h \mathrm{~m}$，杆子与塔之间的距离为 $\mathrm{AC}=x \mathrm{~m}$。这意味着，$\mathrm{AE}=50-h \mathrm{~m}$$\mathrm{AC}=\mathrm{DE}=x \mathrm{~m}$我们知道，$\tan \theta=\frac{\text { 对边 }}{\text { 邻边 }}$$=\frac{\text ... 阅读更多
已知：两棵不同高度的树之间的水平距离为 \( 60 \mathrm{~m} \)。从第二棵树顶端看第一棵树顶端的俯角为 \( 45^{\circ} \)。第二棵树的高度为 \( 80 \mathrm{~m} \) 解题步骤：我们必须找到第一棵树的高度。解答：设 AB 和 CD 为两棵树，第二棵树的高度 AB=80 米。设第一棵树的高度 CD=h 米。两棵树之间的距离，AC = 60 米。从图中，AC=DE= 60 米，AE=CD=h，BE = 80-h…… 阅读更多
从灯塔顶端观察两艘船，它们在灯塔的同一侧，俯角分别为 \( 45^{\circ} \) 和 \( 30^{\circ} \)。如果两艘船相距 \( 200 \mathrm{~m} \)，求灯塔的高度。
已知：从灯塔顶端观察两艘船，它们在灯塔的同一侧，俯角分别为 \( 45^{\circ} \) 和 \( 30^{\circ} \)。两艘船相距 \( 200 \mathrm{~m} \)。解题步骤：我们必须找到灯塔的高度。解答：设 AB 为灯塔的高度，C、D 为两艘船，一前一后。从图中，$\mathrm{CD}=200 \mathrm{~m}, \angle \mathrm{BCA}=30^{\circ}, \angle \mathrm{BDA}=45^{\circ}$设灯塔的高度为 $\mathrm{AB}=h \mathrm{~m}$，第一艘船 D 与灯塔之间的距离为…… 阅读更多
已知：从塔基同一水平线上两点观察塔顶的仰角互余，这两点与塔基的距离分别为$4\ m$和$9\ m$。
已知：灯塔高$200\ m$，从灯塔顶端观察两侧船只的俯角分别为$60^{o}$和$45^{o}$。
已知：两根杆子之间的水平距离为\( 15 \mathrm{~m} \)。从第二根杆子顶端观察第一根杆子顶端的俯角为\( 30^{\circ} \)。第二根杆子高\( 24 \mathrm{~m} \)