数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法学研究
已知：一个菱形，其对角线分别为 16 厘米和 12 厘米。求解：求菱形的周长。解：在对角线互相平分的点 O 处，形成的角为 90°。菱形的对角线 = 12 厘米和 16 厘米因此，对角线 BD 的一半 = OB = 1/2 × 12 = 6 厘米 对角线 AC 的一半 = 1/2 × 16 = 8 厘米在三角形 OBC 中，OB = 6 厘米，OC = 8 厘米，∠BOC = 90° 使用勾股定理，菱形的边 a = √(p²+b²) a = √(6²+8²) = √(36+64) = √100 = 10 厘米已知，菱形的周长 = 4a = 4 × 10 = 40 厘米因此，菱形的周长为 40 厘米。
已知：一个六边形。求解：求六边形的对角线条数，并通过绘制草图进行验证。解：n 边形中的对角线条数 = n(n-3)/2在六边形中，边数 n = 6因此，六边形的对角线条数 = 6(6-3)/2 = 9因此，六边形有 9 条对角线。
已知：PQRS 是一个梯形，其中 PQ || SR，∠P = 130°，∠Q = 110°。求解：求 ∠R 和 ∠S。解：在梯形 PQRS 中，相邻角互补⇒ P + S = 180° ⇒ 130° + S = 180° ⇒ S = 180° - 130° = 50°类似地，∠Q 和 ∠R 也是相邻角。⇒ Q + R = 180° ⇒ 110° + R = 180° ⇒ R = 180° - 110° = 70°因此，∠R = 70° 和 ∠S = 50°。
"\已知：在给定图形中，ABCD 是一个菱形，其对角线相交于点 O。求解：求 x。解：在三角形 OCD 中，OD = 12 厘米，OC = (x - 2)，CD = (x + 6)∠COD = 90° [在菱形中，对角线在交点处形成 90° 角]使用勾股定理，CD² = OC² + OD² ⇒ (x + 6)² = (x - 2)² + 12² ⇒ x² + 12x + 36 = x² - 4x + 4 + 144 ⇒ 12x + 4x = 148 - 36 ⇒ 16x = 112 ⇒ x = 112/16 ⇒ x = 7 因此，x = 7。
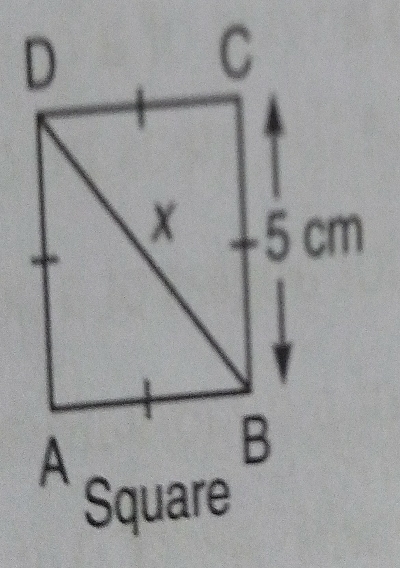
已知：边长为 5 厘米的正方形 ABCD。求解：求 x 的值。解：如给定，ABCD 是一个正方形。因此，AB = BC = CD = DA = 5 厘米，对角线 BD = x。使用勾股定理，BD² = BC² + CD² ⇒ x² = BC² + CD² ⇒ x² = 5² + 5² ⇒ x² = 25 + 25 ⇒ x² = 50 ⇒ x = √50 ⇒ x = 5√2。
已知：平行四边形的周长为 25 厘米，较长边的长度为 8 厘米。求解：求较短边的长度。解：设平行四边形的另一边为 x。∴ 周长 = 2(l + b) ⇒ 2(8 厘米 + x) = 25 厘米 ⇒ 16 厘米 + 2x = 25 厘米 ⇒ 2x = 25 厘米 - 16 厘米 ⇒ 2x = 9 厘米 ⇒ x = 9/2 厘米 ⇒ x = 4.5 厘米因此，较短边的长度为 4.5 厘米。
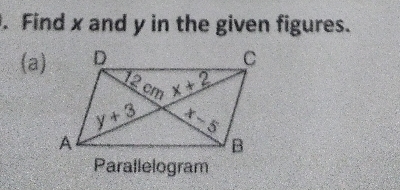
"\已知：ABCD 是一个平行四边形。求解：求 x 和 y。解：因为 ABCD 是一个平行四边形，所以对角线 AC 和 BD 相等。并且形成两个全等三角形。⇒ y + 3 = x + 2 ⇒ x - y = 1 ........ (i) 并且 x - 5 = 12 ⇒ x = 12 + 5 = 17，将 x = 17 代入 (i)，17 - y = 1 ⇒ y = 17 - 1 ⇒ y = 16 因此，x = 17，y = 16。
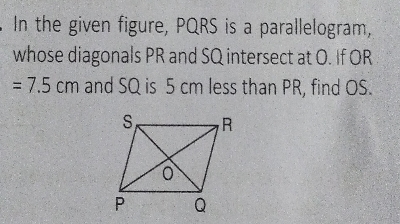
已知：在给定的图形中，PQRS 是一个平行四边形，其对角线 PR 和 SQ 相交于 O。OR = 7.5 厘米，SQ 比 PR 短 5 厘米。求解：求 OS。解：因为在平行四边形中，对角线互相平分。OR = 7.5，则 OP 也将是 7.5。因此，PR = 7.5 + 7.5 = 15 厘米由于 SQ = PR - 5 ⇒ SQ = 15 - 5 = 10 厘米 ⇒ OQ = OS = SQ/2 = 5 厘米
求解：求书的周长。解：如果 l 是书的长度，b 是书的宽度。书的周长 = 2(l + b)。
已知：正五边形 ABCDE 和正方形 ABFG 在 AB 的相对两侧形成。求解：求 ∠BCF。解：如给定，ABCDE 是一个正五边形，ABFG 是一个正方形。所以五边形和正方形的边长相等。正方形的每个角 = 90°正五边形的每个角 = 108°从图中，∠FBC = 360° - (∠ABF + ∠ABC) ⇒ ∠FBC = 360° - (90° + 108°) ⇒ ∠FBC = 360° - 198° = 162°在三角形 BCF 中，因为 BF = FC ∴ BFC = BCF ⇒ ∠BCF + ∠BCF + 162° = 180° ⇒ 2∠BCF = 180° - 162° ⇒ ∠BCF = 18°/2 ⇒ ∠BCF = 9° 阅读更多