已知:正多边形的内角和为 $1260^{\circ}$。求解:求该多边形的边数。解:已知,多边形内角和 = $(2n-4) \times 90^o$ 已知,内角和 = $1260^o$ $\Rightarrow 1260 = (2n-4) \times 90^o$ $\Rightarrow 2n-4 = \frac{1260}{90}$ $\Rightarrow 2n-4 = 14$ $\Rightarrow 2n = 18$ $\Rightarrow n = 9$ 因此,多边形的边数为 9。
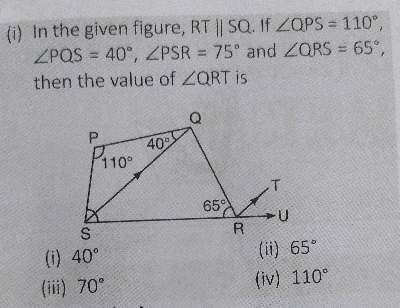
已知:在给定图形中,$RT \parallel SQ$。如果 $\angle QPS = 110^{\circ}$,$\angle PQS = 40^{\circ}$,$\angle PSR = 75^{\circ}$ 且 $\angle QRS = 65^{\circ}$。求解:求 $\angle QRT$ 的值。解:从图中,在 $\triangle PQS$ 中,$\angle PQS + \angle QPS + \angle PSQ = 180^o$ $\Rightarrow \angle PSQ = 180^o - \angle QPS - \angle PQS = 180^o - 110^o - 40^o = 30^o$ 已知 $\angle PSR = 75^o$ $\Rightarrow \angle PSQ + \angle QSR = 75^o$ $\Rightarrow \angle QSR = 75^o - \angle PSQ = 75^o - 30^o = 45^o$ 在 $\triangle QSR$ 中 $\angle QRS + \angle PSQ + \angle SQR = 180^o$ $\angle SQR = 180^o - \angle QRS - \angle QSR = 180^o - 65^o - 45^o = 70^o$ 由于 $RT \parallel SQ$,$\angle QRT = \angle SQR = 70^o$ [因为内错角] 阅读更多
已知:$ABCD$ 是一个矩形。对角线 $AC$ 和 $BD$ 相交于 $O$ 点,且 $OA = x + 2$,$OC = 2x - 1$。求解:求 $x$ 的值。解:$OA = OB$ [对角线互相平分] $\Rightarrow x + 2 = 2x - 1$ $\Rightarrow 2x - x = 2 + 1$ $\Rightarrow x = 3$
已知:$ABCD$ 是一个正方形,$\angle ABD = 45^{\circ}$。求解:求 $x, y$ 和 $z$。解:已知,$ABCD$ 是一个正方形。在正方形中,对角线互相垂直平分。$\Rightarrow y = \angle AOB = 90^o$ 在 $\triangle OAB$ 中,$\angle OAB = 180^o - (45^o + 90^o) = 45^o$ $AB \parallel CD$,$\therefore \angle CAB = \angle DCO = z = 45^o$ 且 $x + \angle OAB = 90^o$ $\Rightarrow x + 45^o = 90^o$ $\Rightarrow x = 45^o$ 因此,$x = 45^o$,$y = 90^o$ 且 $z = 45^o$。
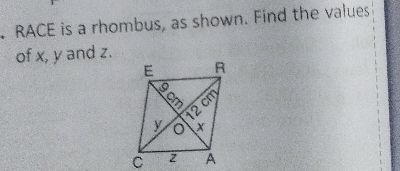
已知:$RACE$ 是一个菱形,如图所示。求解:求 $x, y$ 和 $z$。解:因为 $RACE$ 是一个菱形。所以对角线 $RC$ 和 $AE$ 互相垂直平分。$\Rightarrow OC = OR$ 且 $OA = OE$ $\Rightarrow y = 12\ cm$ 且 $x = 9\ cm$ 在直角 $\triangle AOC$ 中,根据勾股定理,$z^2 = x^2 + y^2$ $\Rightarrow z^2 = 9^2 + 12^2$ $\Rightarrow z^2 = 81 + 144$ $\Rightarrow z^2 = 225$ $\Rightarrow z = \sqrt{225}$ $\Rightarrow z = 15\ cm$ 因此,$x = 9\ cm$,$y = 12\ cm$ 且 $z = 15\ cm$。
求解:找出三对质数,它们的差为 2。解:只能被 1 或自身整除的数称为质数。因此,质数可以是 2、3、5、7、11、13、17、19…… 因此,三对差为 2 的质数是:(i) (5, 7) (ii) (11, 13) (iii) (17, 19)
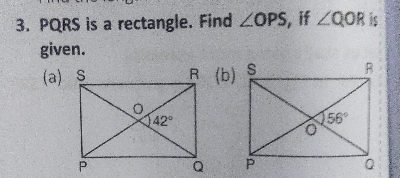
已知:$PQRS$ 是一个矩形。求解:如果 $\angle QOR$ 为:(a) $42^o$ (b) $56^o$,求 $\angle OPS$。解:(a) 因为 $PQRS$ 是一个矩形,因此对角线 $PR$ 和 $QS$ 等长。$\therefore \frac{1}{2}PR = \frac{1}{2}QS$ $\Rightarrow OS = OP\ .......\ (i)$ 在 $\triangle OPS$ 中 $\angle POS = \angle QOR = 42^o$ [已知] $\angle OSP = \angle OPS$ [因为 $OS = OP$] $\therefore \angle POS + \angle OPS + \angle OPS = 180^o$ $\Rightarrow 42^o + 2\angle OPS = 180^o$ $\Rightarrow 2\angle OPS = 138^o$ $\Rightarrow \angle OPS = 69^o$ (b) 同理,当 $\angle QOR = 56^o$ 时 $\Rightarrow 2\angle OPS = 180^o - 56^o$ $\Rightarrow 2\angle OPS = 124^o$ $\Rightarrow \angle OPS = 62^o$ 阅读更多
已知:一根垂直的塔矗立在水平面上,塔顶上有一面高 \( 7 \mathrm{~m} \) 的旗杆。从平面上的一点,旗杆底部的仰角为 \( 30^{\circ} \),旗杆顶部的仰角为 \( 45^{\circ} \)。求解:我们需要求塔的高度。解:设 AB 为塔,BC 为旗杆的长度。设 D 为观察点。从图中,$\mathrm{BC} = 7 \mathrm{~m}$,$\angle \mathrm{BDA} = 30^{\circ}$,$\angle \mathrm{CDA} = 45^{\circ}$ 设塔的高度为 $\mathrm{DB} = h \mathrm{~m}$,观察点与塔的距离为… 阅读更多
已知:底边 $BC = 7\ cm$,$\angle B=75^o$,两边之和 $AB+AC=12\ cm$。 求作:$\vartriangle ABC$。

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
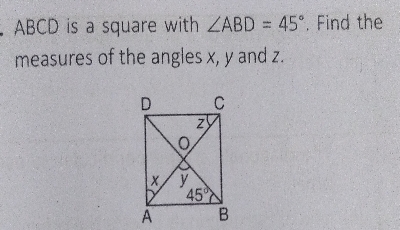 "\
"\ "\
"\