已知:从塔顶观察烟囱顶部的仰角为 \( 60^{\circ} \),从塔顶观察烟囱底部的俯角为 \( 30^{\circ} \)。塔高为 \( 40 \mathrm{~m} \)。根据污染控制规范,排烟烟囱的最低高度应为 \( 100 \mathrm{~m} \)。需要做的事情:我们必须找到烟囱的高度,并说明上述烟囱的高度是否符合污染规范。解决方案: 设 $AB$ 为塔,$CD$ 为 ... 阅读更多
已知:竖直杆的影子长度等于其高度。需要做的事情:我们必须找到太阳的仰角 解决方案: 设 $AB$ 为杆,$AC$ 为影子。设杆的高度为 $\mathrm{AB}=h \mathrm{~m}$,影子的长度为 $\mathrm{AC}=h \mathrm{~m}$。设仰角为 $\theta$。我们知道,$\tan \theta=\frac{\text { 对边 }}{\text { 邻边 }}$$=\frac{\text { AB }}{AC}$$\Rightarrow \tan \theta=\frac{h}{h}$$\Rightarrow \tan \theta=1$$\Rightarrow \tan \theta=\tan 45^{\circ}$$\Rightarrow \theta=45^{\circ}$ [因为 $\tan 45^{\circ}=1$]因此,仰角为 $45^{\circ}$。 阅读更多
已知:一架飞机在 $210\ m$ 的高度飞行。在某一时刻,飞机在该高度飞行时,观察到河两岸相反方向同一直线上的两点的俯角分别为 $45^{\circ}$ 和 $60^{\circ}$。 需要做的事情:我们必须找到河流的宽度。解决方案:设飞机的高度为 $AB=210\ m$。设 $C$ 和 $D$ 为河两岸相反方向同一直线上的两点。两点 $C$ 和 $D$ 的俯角分别为 $60^{o}$ 和 $45^{o}$。$\angle BCA=60^{o}$ 和 $\angle ... 阅读更多
已知:悬崖两侧的两人观察到悬崖顶部的仰角分别为 \( 30^{\circ} \) 和 \( 60^{\circ} \),悬崖高 \( 80 \mathrm{~m} \)。需要做的事情:我们必须找到两人之间的距离。解决方案: 设 $AB$ 为悬崖,$C, D$ 为悬崖两侧的两人。从图中,$\mathrm{AB}=80 \mathrm{~m}, \angle \mathrm{BCA}=30^{\circ}, \angle \mathrm{BDA}=60^{\circ}$。设点 $A$ 和点 $C$ 之间的距离为 $\mathrm{CA}=x \mathrm{~m}$,点 $A$ 和点 $D$ 之间的距离为 $\mathrm{AD}=y \mathrm{~m}$。我们知道,$\tan \theta=\frac{\text { 对边 }}{\text ... 阅读更多
已知:一棵树因暴风雨而折断,折断的部分弯曲,使树顶触地,与地面成 \( 30^{\circ} \) 角。树根到树顶触地处的距离为 \( 10 \mathrm{~m} \)。需要做的事情:我们必须找到树的高度。解决方案: 设 $AB$ 为树的原始高度,$CD$ 为折断的部分,它在 $D$ 处触地。设点 $D$ 为折断树枝的顶部触地的点。从 ... 阅读更多
已知:一个气球通过一根长 \( 215 \mathrm{~m} \) 的缆绳与气象地面站相连,缆绳与水平面成 \( 60^{\circ} \) 角。需要做的事情:我们必须确定气球离地面的高度。解决方案: 设 $C$ 为气象地面站,$AB$ 为气球离地面的高度。从图中,$\mathrm{BC}=215 \mathrm{~m}, \angle \mathrm{BCA}=60^{\circ}$设气球离地面的高度为 $\mathrm{AB}=h \mathrm{~m}$。我们知道,$\sin \theta=\frac{\text { 对边 }}{\text { 斜边 }}$$=\frac{\text { AB }}{BC}$$\Rightarrow \sin 60^{\circ}=\frac{h}{215}$$\Rightarrow \frac{\sqrt3}{2}=\frac{h}{215}$$\Rightarrow (215)\frac{\sqrt3}{2}=h \mathrm{~m}$$\Rightarrow h=\frac{215(1.732)}{2} \mathrm{~m}$$\Rightarrow h=185.975 \mathrm{~m}$$\Rightarrow h=186 \mathrm{~m}$因此,气球的高度 ... 阅读更多
已知: $ 7 t^{2} \div 28(t m)^{3} $.需要做的事情:计算 $7 t^{2} \div 28(t m)^{3}$。 解决方案:如给定,$7t^{2} \div 28( tm)^{3}$$=7t^2\div 28t^3m^3$$=\frac{7t^2}{28t^3m^3}$$=\frac{1}{4}\times t^{2-3}m^{-3}$$=4^{-1}t^{-1}m^{-3}$因此,$ 7 t^{2} \div 28(t m)^{3}=4^{-1}t^{-1}m^{-3}$。
已知:一座塔矗立在水平地面上,当太阳高度角为\( 30^{\circ} \)时,其影长比太阳高度角为\( 45^{\circ} \)时长\( 2 x \)米。要求:我们必须证明塔高为\( x(\sqrt{3}+1) \)米。解答:设塔高为$AB$,当太阳高度角为\( 30^{\circ} \)时的影长为$CA$,当太阳高度角为\( 45^{\circ} \)时的影长为$DA$。从图中,$\mathrm{CD}=2x \mathrm{~m}, \angle \mathrm{BCA}=30^{\circ}, \angle \mathrm{BDA}=45^{\circ}$设塔高为$\mathrm{AB}=h \mathrm{~m}$,影长... 阅读更多
已知:在给定图形中,$OC$和$OD$分别是$\angle BCD$和$\angle ADC$的角平分线,且$\angle A=105^{\circ}$。要求:求$\angle B$。解答:$\because OD$是$ADC$的角平分线$\therefore OC$是$BCD$的角平分线$\Rightarrow \angle ADC=\angle D=\angle ODC\times 2$$\Rightarrow \angle D=25^o\times 2=50^o$类似地:$\angle BCD=\angle C=OCD\times 2$$\Rightarrow \angle C=30^o\times 2=60^o$已知$A+B+C+D=360^o$ $( 四边形的内角和=360^o )$$\Rightarrow 105^o+B+60^o+50^o=360^o$$\Rightarrow 105^o+B+110^o=360^o$$\Rightarrow B+105^o+110^o=360^o$$\Rightarrow B+215^o=360^o$$\Rightarrow B=360^o - 215^o$$\Rightarrow B=145^o$因此,$\angle B=145^o$。 阅读更多
已知:正多边形的每个内角是其外角的四倍。要求:求该多边形的边数。解答:设边数为$n$,则每个内角$=\frac{( n-2)}{n}\times180$已知外角$=\frac{360}{n}$根据题意,$\frac{( n-2)}{n}\times180=4\times\frac{360}{n}$$\Rightarrow ( n-2)\times 180=4( 360)$$\Rightarrow n-2=\frac{4\times360}{180}$$\Rightarrow n-2=8$$\Rightarrow n=8+2=10$。因此,多边形的边数为$10$。

 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
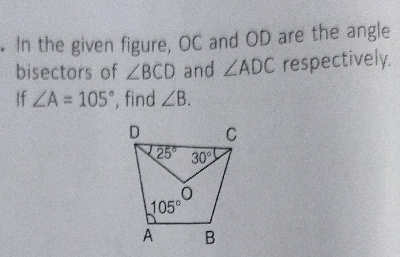 "\
"\