一架飞机在 210 米的高度飞行。在某一时刻，飞机在这个高度上观察到河两岸相反方向的两个点的俯角分别为 45° 和 60°。求这条河的宽度。（使用 $\sqrt3=1.73$）

已知

一架飞机在 210 米的高度飞行。在某一时刻，飞机在这个高度上观察到河两岸相反方向的两个点的俯角分别为 45° 和 60°。

要求

我们需要求出这条河的宽度。

解答

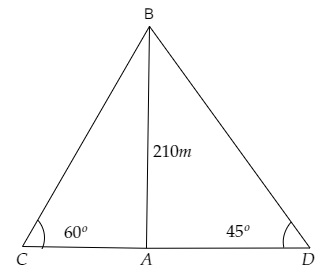
假设飞机在 $AB=210\ m$ 的高度飞行。设 $C$ 和 $D$ 是河两岸相反方向的两个点，且在同一条直线上。

两个点 $C$ 和 $D$ 的俯角分别为 60° 和 45°。

$\angle BCA=60^{o}$ 和 $\angle BDA=45^{o}$

在 $\vartriangle BCA$ 中，

$tan 60^{o}=\frac{AB}{CA}$

$\sqrt{3}=\frac{210}{CA}$

$CA=\frac{210}{\sqrt3} \ m$

在 $\vartriangle BAD$ 中，

$tan45^{o}=\frac{AB}{AD}$

$1=\frac{210}{AD}$

$AD=210\ m$

因此，

河的宽度 $CD=CA+AD=210+\frac{210}{\sqrt3}$

$=\frac{210\sqrt3+210}{\sqrt3}\ m$

$=\frac{210(1.73+1)}{1.73}\ m$

$=\frac{210(2.73)}{1.73}\ m$

$=\frac{573.3}{1.73}\ m$

$=331.38\ m$

因此，河的宽度为 331.38 米。

教程点

更新于: 2022年10月10日

3K+ 浏览量

开启你的 职业生涯

通过完成课程获得认证

开始学习