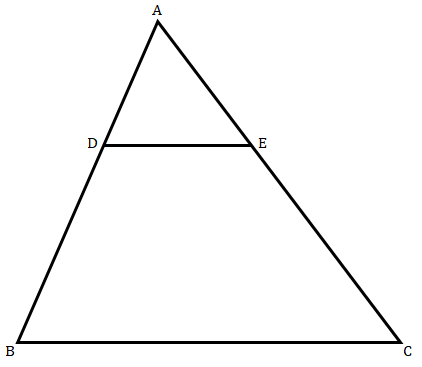
已知:在△ABC 中,D 和 E 分别是 AB 和 AC 的中点。
已知:在给定图形中,DE∥BC 且 DE:BC = 3:5。
已知:给定的等差数列为 -12,-9,-6,……,21。
已知:两根等高的杆子,杆子之间的距离为 80 米。从某一点到杆子顶端的仰角为 60° 和 30°
已知:圆的切线。
已知:两个正方形的面积之和 = 400 cm²,周长之差 = 16 cm。
已知:表达式 1/(2a + b + 2x) = 1/(2a) + 1/b + 1/(2x)
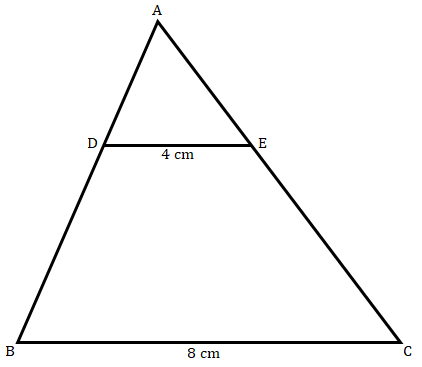
**已知:**如图所示,$DE\ ||\ BC$。$DE\ =\ 4\ m$,$BC\ =\ 8\ cm$,$ΔADE$的面积为$25\ cm^2$。**求:**求$ΔABC$的面积。**解:**在$ΔADE$和$ΔABC$中,$\angle ADE = \angle ABC$(对应角)$\angle DAE = \angle BAC$(公共角)因此,$ΔADE ~ ΔABC$(根据AA相似)我们知道,两个相似三角形的面积之比等于它们对应边平方之比。因此,$\frac{ΔADE的面积}{ΔABC的面积} = (\frac{DE}{BC})^2$$\frac{25}{ΔABC的面积} = (\frac{4}{8})^2$$ΔABC的面积 = \frac{64 \times 25}{16}$$ΔABC的面积 = 100\ cm^2$ $ΔABC$的面积为$100\ cm^2$。
**已知:**一个圆心为O的圆,两条平行切线l和m分别与圆相切于A和B。另一条切线在C点与圆相切,分别与l和m相交于D和E。**求证:**$\angle DOE=90^{o}$**证明:**l和m是圆的两条平行切线,圆心为O,分别与圆相切于A和B。DE是过C点的切线,分别与l和m相交于D和E。步骤如下:连接OC。在$\vartriangle ODA$和$\vartriangle ODC$中,$OA=OC\ \ \ \ \ \ \ \ \ \ \ \ \ \ ... 阅读更多
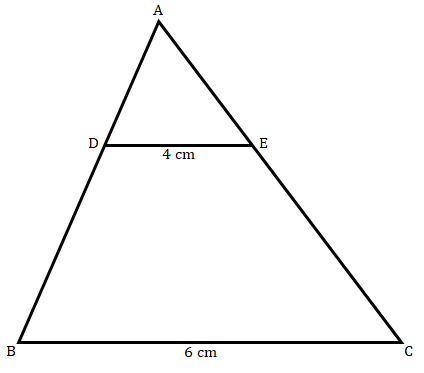
**已知:**如图所示,$DE\ ||\ BC$。$DE\ =\ 4\ m$,$BC\ =\ 6\ cm$,$ΔADE$的面积为$16\ cm^2$。**求:**求$ΔABC$的面积。**解:**在$ΔADE$和$ΔABC$中,$\angle ADE = \angle ABC$(对应角)$\angle DAE = \angle BAC$(公共角)因此,$ΔADE ~ ΔABC$(根据AA相似)我们知道,两个相似三角形的面积之比等于它们对应边平方之比。因此,$\frac{ΔADE的面积}{ΔABC的面积} = (\frac{DE}{BC})^2$$\frac{16}{ΔABC的面积} = (\frac{4}{6})^2$$ΔABC的面积 = \frac{36 \times 16}{16}$$ΔABC的面积 = 36\ cm^2$ $ΔABC$的面积为$36\ cm^2$。

 数据结构
数据结构 网络
网络 关系型数据库管理系统
关系型数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP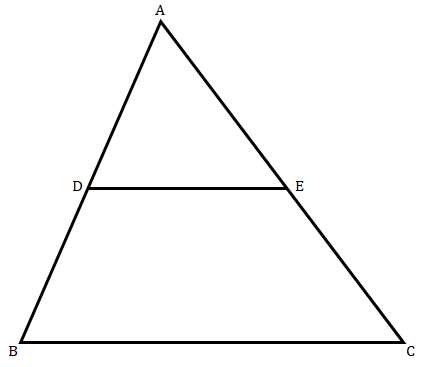 "\
"\
 "\
"\ "\
"\ "\
"\