数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
已知：表达式： $x^{2} -3\sqrt{5} \ x+10=0$ 求解：求解给定二次方程的根。 解：我们知道，对于二次方程 $ax^{2} +bx+c=0$ $x=\frac{-b\pm \sqrt{b^{2} -4ac}}{2a}$ 将其与给定的二次方程比较，可得 $a=1, b=-3\sqrt{5} \ 和\ c=10$ 代入这些值 $\displaystyle a, \ b\ 和\ c$ $x=\frac{-( -3\surd 5) \pm \sqrt{( -3\surd 5)^{2} -4\times 1\times 10}}{2\times 1}$ $x=\frac{3\sqrt{5} \pm \sqrt{( 45-40)}}{2}$ $x=\frac{\left( 3\sqrt{5} \pm \sqrt{5}\right)}{2}$ 如果 $x=\frac{\left( 3\sqrt{5} +\sqrt{5}\right)}{2}$ $\Rightarrow x=\frac{4\sqrt{5}}{2} $ $\Rightarrow x=2\sqrt{5}$ 如果 $x=\frac{\left( 3\sqrt{5} -\sqrt{5}\right)}{2}$ $\Rightarrow x=\frac{\left( 2\sqrt{5}\right)}{2}$ $\Rightarrow x=\sqrt{5}$ $\therefore x=2\sqrt{5}, \ \sqrt{5}$ 阅读更多
已知：一个等差数列，它的第四项，$a_{4} =9$ 第六项和第十三项的和，$a_{6} +a_{13} =40$ 求解：求该等差数列。 解： 设给定等差数列的首项为$\ a\ $，公差为 $d.$ 已知等差数列的第 n 项，$a_{n} =a+( n-1) d$ $a_{4} =a+( 4-1) d $ $( 这里\ a_{4} =9\ 和\ n=4) $ $\Rightarrow a+3d=9$ $\ \ \ \ \dotsc \dotsc \dotsc ..( 1)$ 类似地$\ a_{6} =a+( 6-1) d=a+5d$ 和 $a_{13} =a+( 13-1) d=a+12d\ \ ... 阅读更多
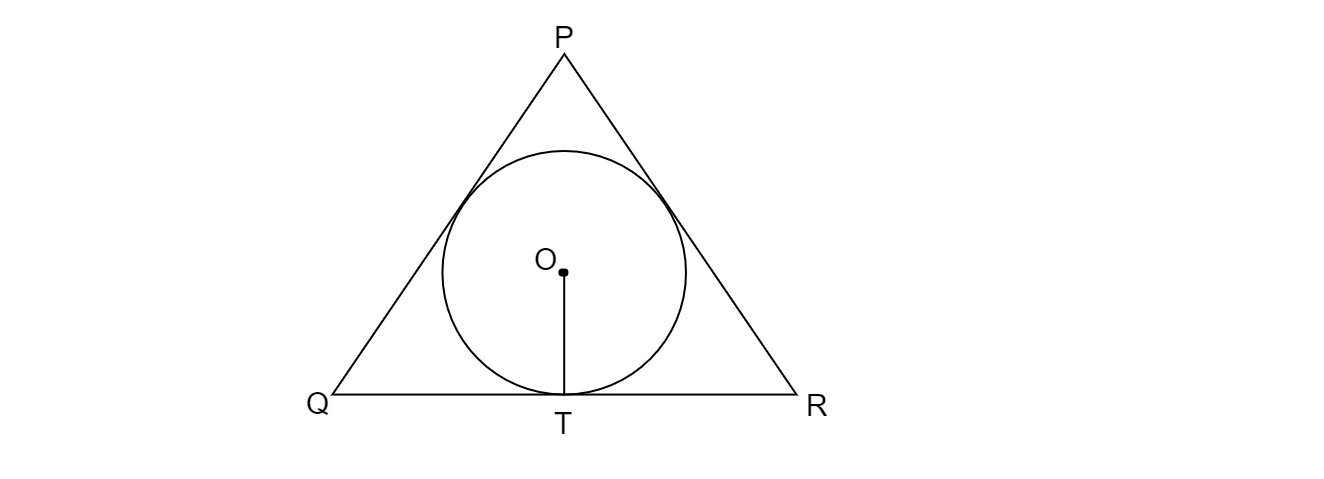
"\已知：一个圆心为 O、半径为 6 厘米的圆，一个外接该圆的三角形 PQR，T 是切点，将 $\displaystyle QR\ $ 分成 QT=12 cm 和 TR=9 cm 两段。三角形的面积 = $189 \ cm^{2}$。 求解：求出 PQ 和 PR 的长度。 解：连接 OP、OM、ON、OQ 和 OR。$PQ=PN+QN$ $PR=PM+MR$ 因为 PQ 和 PR 是圆的切线，所以 $PN=PM$ 和 $\ QN=QT$ 和 $MR=TR$ 这里给定三角形的面积 $\ =\ 189\ cm^{2}$，三角形 $\vartriangle PQR$ 的底，$QR=QT+TR=12+9=21cm$ 已知三角形的面积 $=\frac{1}{2} \times base\times height$ $189=\frac{1}{2} \times ... 阅读更多
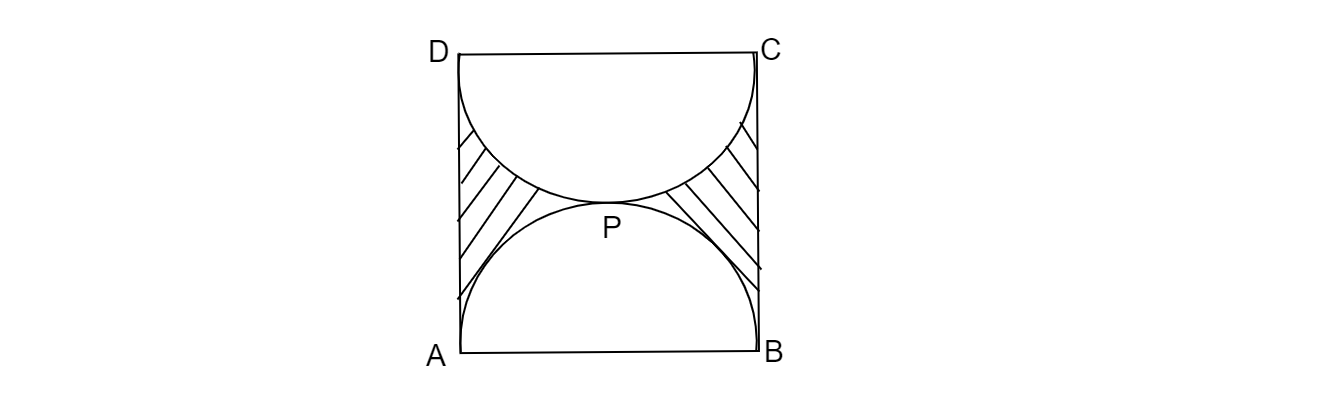
"\已知：图 4，其中 ABCD 是边长为 14 厘米的正方形，APB 和 CPD 是两个半圆。 求解：求阴影区域的周长。 解：由上述问题可知，ABCD 是正方形，APB 和 CPD 是两个半圆。 $\because ABCD$ 是正方形。 $\because$ 正方形 ABCD 的边长为 14 厘米。 $\therefore AB=BC=CD=DA=14\ cm$ 这里 AB 和 CD 是半圆 APB 和 CPD 的直径。 $\therefore$ 半圆 APB 和 CPD 的半径 $=\frac{14}{2}$ $\therefore$ 弧 APB 的长度 $=\frac{弧的度数}{360^{0}} \times 弧的半径=\frac{180^{o}}{360^{o}} \times \frac{4}{2} =3.5\ cm$ 同理，弧 CPD 的长度 = 弧 APB 的长度 = 3.5 cm 周长 ... 阅读更多
已知：一条线段 AB 长度为 7 厘米。 求解：画出线段 AB，并使用尺规作图，在线段 AB 上找到一点 P，使得 $\frac{AP}{AB} =\frac{3}{5}$。 解：上述问题给定了一条长度为 7 厘米的线段 AB。首先使用尺子画出 $AB=7$ 厘米 已知在 AB 线段上有一点 P。并且 $\frac{AP}{AB} =\frac{3}{5}$ $\Rightarrow AP=\frac{3}{5} AB$ 我们知道 $AB=AP+PB$ $\therefore PB=AB-AP=AB-\frac{3}{5} AB=\frac{2}{5} AB$ 那么 $\frac{AP}{PB} =\frac{\frac{3}{5} AB}{\frac{2}{5} AB} =\frac{3}{2}$ 现在按照步骤找到给定 ... 阅读更多
已知：方程 $mx( x-7) +49=0$。 求解：求出 m 的值，使得该方程有两个相等的根。 解：给定方程为 $mx( x-7) +49=0$ $\Rightarrow mx^{2} -7mx+49=0$ 将其与二次方程 $ax^{2} +bx+c=0$ 比较 我们发现 $a=m, \ b=-7m\ 和\ c=49$ 为了使二次方程有两个相等的根，其判别式 D$=0$ 或者 $\sqrt{\left( b^{2} -4ac\right)} \ =0$ 代入 $\ a, \ b\ 和\ c$ 的值 $\sqrt{\left(( -7m)^{2} -4\times m\times 49\right)} =0$ $\Rightarrow \sqrt{\left( 49m^{2} -196m\right)} =0$ $\Rightarrow 49m^{2} -196m=0$ 或 $49\left( m^{2} -4m\right) =0$ $m^{2} -4m=0$ $\Rightarrow m( ... 阅读更多
已知：从 10 到 99 的两位数。 求解：求能被 6 整除的两位数。 解：一个两位数能被 6 整除，则它必须同时能被 2 和 3 整除。 条件 1. 它必须是偶数，才能被 2 整除。 条件 2. 它的数字之和必须能被 3 整除。并且该数本身必须能被 3 整除。 从 10 开始。10 是偶数，所以能被 2 整除，但不能被 3 整除。所以它不能被 ... 阅读更多
"\已知：一个圆与一个四边形 ABCD 的所有四条边相切，四边形的边长为 AB=6 厘米，BC=9 厘米，CD$=8$ 厘米（如图所示）。 求解：求 AD$=?$ 解： AB$=6\ $厘米 BC$=9\ $厘米 CD$=8$ 厘米 AD$=?$ AB、BC、CD、AD 是圆的切线，并且 AP$=$AS，RD$=$DS BP$=$BQ，AS$=$AP CQ$=$CR AB$=$AP$+$PB$=$ AP$+$PQ \ ……………….$( 1)$ BC$=$BQ$+$QC ……………………….. $( 2)$ CD$=$RC$+$DR …………………………$( 3)$ AD$=$AS$+$DS ………………………..$( 4)$ 将 $( 1) ,\ ( 2) ,\ ( 3) ,\ ( 4)$ 相加 6$+$9$+$8$+$AD$=$AP$+$AS$+$BP$+$BQ$+$CQ$+$RC$+$RD$+$DS 23$+$AD$=2( AP) +2( BP) +2( RC) +2( RD)$ $23+AD=2( AB) +2( CD)$ $AD\ =5$ 厘米
已知：连接点 $A( -6, \ 5)$ 和 $B( -2, \ 3)$ 的线段，以及它的中点 $P\left(\frac{a}{2} ,\ 4\right)$ 求解：求出 $a=?$ 解：如果有一条连接两点 $ ( x_{1} ,\ y_{1} )$ 和 $( x_{2} ,\ y_{2})$ 的线段，则它的中点 $( x, \ y) =\left(\frac{x_{1} +x_{2}}{2} ,\ \frac{y_{1} +y_{2}}{2}\right)$ 同理 $P\left(\frac{a}{2} ,4\right) =\left(\frac{-6-2}{2} ,\frac{5+3}{2}\right)$ $\Rightarrow \ P\left(\frac{a}{2} ,4\right) =\left(\frac{-8}{2} ,\frac{8}{2}\right)$ $\Rightarrow \ P\left(\frac{a}{2} ,4\right) =\left(\frac{-8}{2} ,4\right)$ $\Rightarrow \frac{a}{2} =\frac{-8}{2}$ $\Rightarrow a=-4$ $\therefore$ 选项 $( A)$ 正确。 阅读更多
已知：给出两点 A(-6, 7) 和 B(-1, -5)。 求：求距离 2AB=?