数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
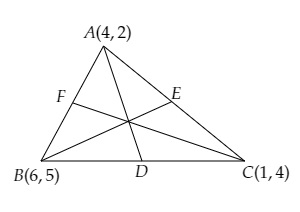
法律研究已知$\triangle ABC$的顶点为$A (4, 2), B (6, 5)$和$C (1, 4)$。在中线BE和CF上分别找到点Q和R，使得$BQ : QE = 2 : 1$和$CR : RF = 2 : 1$。你观察到了什么？
已知
$\triangle ABC$的顶点为$A (4, 2), B (6, 5)$和$C (1, 4)$。
$BQ : QE = 2 : 1$和$CR : RF = 2 : 1$。
要求
我们需要找到中线BE和CF上点Q和R的坐标。
解答
$D$是BC的中点。
这意味着，
使用中点公式，我们得到：
$D$的坐标为$(\frac{6+1}{2}, \frac{5+4}{2})$
$=(\frac{7}{2},\frac{9}{2})$
类似地，
$E$的坐标为$(\frac{4+1}{2}, \frac{2+4}{2})$
$=(\frac{5}{2},3)$
$F$的坐标为$(\frac{4+6}{2}, \frac{2+5}{2})$
$=(5,\frac{7}{2})$
$AP : PD = 2 : 1$。
使用分点公式，我们得到：
\( (x,y)=(\frac{m x_{2}+n x_{1}}{m+n}, \frac{m y_{2}+n y_{1}}{m+n}) \)
$P$的坐标为\( (\frac{2 \times \frac{7}{2}+1 \times 4}{1+2}, \frac{2 \times \frac{9}{2}+1 \times 2}{1+2}) \)
\( =(\frac{7+4}{3}, \frac{9+2}{3}) \)
\( =(\frac{11}{3}, \frac{11}{3}) \)
$BQ : QE = 2 : 1$$Q$的坐标为\( (\frac{2 \times \frac{5}{2}+1 \times 6}{1+2}, \frac{2 \times 3+1 \times 5}{1+2}) \)
\( =(\frac{5+6}{3}, \frac{6+5}{3}) \)
\( =(\frac{11}{3}, \frac{11}{3}) \)
$CR : RF = 2 : 1$
$R$的坐标为\( (\frac{2 \times 5+1 \times 1}{1+2}, \frac{2 \times \frac{7}{2}+1 \times 4}{1+2}) \)
\( =(\frac{10+1}{3}, \frac{7+4}{3}) \)
\( =(\frac{11}{3}, \frac{11}{3}) \)
我们观察到$P, Q$和$R$的坐标相同。$P, Q$和$R$重合。
三角形各边的中线都经过同一点，该点称为三角形的重心。因此，$(\frac{11}{3},\frac{11}{3})$是三角形ABC的重心。
$Q$和$R$的坐标为\( (\frac{11}{3}, \frac{11}{3}) \)。
41 次浏览
