三角形ABC的顶点分别为(-2, 1), (5, 4)和(2, -3)。求三角形的面积和过A点的中线的长度。

已知

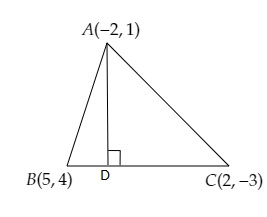
三角形ABC的顶点分别为(-2, 1), (5, 4)和(2, -3)。

要求

我们必须求出三角形的面积和过A点的中线的长度。

解答

设AD为过A点的中线的长度。

我们知道：

顶点为(x₁,y₁), (x₂,y₂), (x₃,y₃)的三角形的面积由下式给出：

三角形面积=½[x₁(y₂-y₃)+x₂(y₃-y₁)+x₃(y₁-y₂)]

因此，

三角形ABC的面积 = ½[-2(4+3)+5(-3-1)+2(1-4)]

= ½[-2(7)+5(-4)+2(-3)]

= ½[-14-20-6]
= ½×(-40)

= -20 = 20 平方单位

BC的长度 = √[(2-5)²+(-3-4)²]

= √[(-3)²+(-7)²]

= √(9+49)

= √58 单位
三角形ABC的面积 = ½ × 底 × 高
=> 20 = ½ √58 × AD
=> AD = (20 × 2) / √58

= 40 / √58
三角形的面积为20平方单位，过A点的中线的长度为40/√58单位。

教程点

更新于：2022年10月10日

浏览量：123

启动你的职业生涯

完成课程获得认证

开始学习