一个孩子在图画纸上制作海报，画了一个边长为 14 厘米的正方形 ABCD。她在以 A、B、C 和 D 为圆心的四个圆圈中，建议了不同的节能方法。这些圆圈的绘制方式使得每个圆圈都与另外三个圆圈中的两个圆圈外切。她在阴影区域写了一条信息“节约能源”。求阴影区域的周长和面积。（使用 π=22/7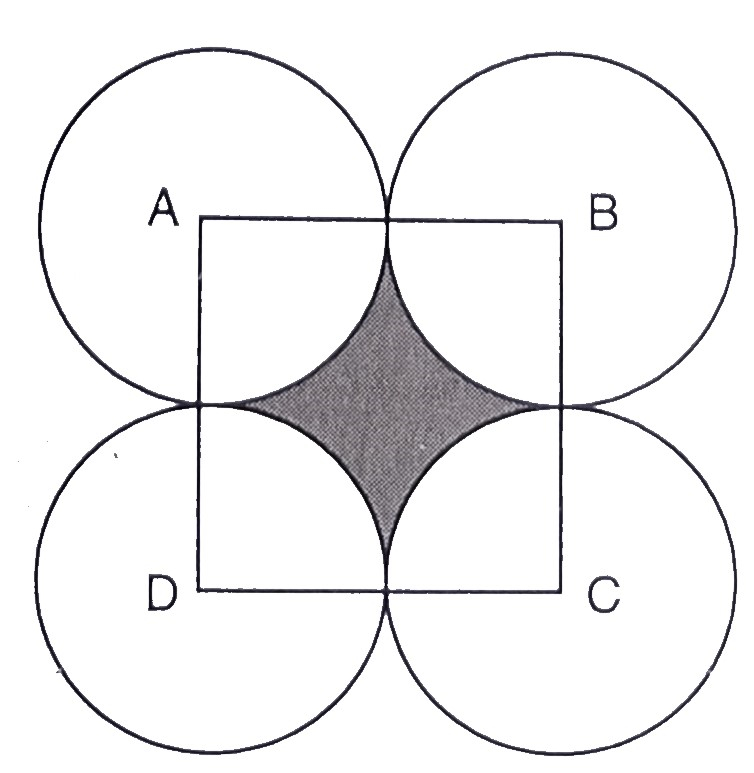）"\n

已知

一个孩子在图画纸上制作海报，画了一个边长为 14 厘米的正方形 ABCD。

她在以 A、B、C 和 D 为圆心的四个圆圈中，建议了不同的节能方法。

这些圆圈的绘制方式使得每个圆圈都与另外三个圆圈中的两个圆圈外切。

要求：

我们必须找到阴影区域的周长和面积。

解答

正方形 ABCD 的边长 = 14 厘米

这意味着，

每个圆的半径 r = 7 厘米

因此，

阴影区域的周长 = 4 × 每个四分之一圆弧的周长

$=4 \times \frac{1}{4}(2 \pi r)$

$=2 \times \frac{22}{7} \times 7$

$=44 厘米$

阴影区域的面积 = 正方形的面积 - 正方形内四个四分之一圆的面积

$=(14)^{2}-4 \times \frac{1}{4} \pi 7^{2}$

$=(14)^{2}-\frac{22}{7} \times 7^2$

$=196-154$

$=42 平方厘米$

阴影区域的周长和面积分别为 44 厘米和 42 平方厘米。

教程点

更新于： 2022 年 10 月 10 日

37 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习