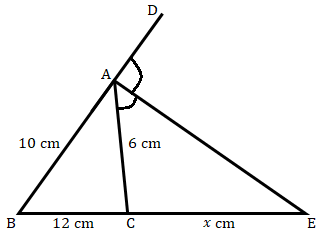
在下图中，$AE$ 是外角 $∠\ CAD$ 的平分线，与 $BC$ 的延长线交于点 $E$。如果 $AB\ =\ 10\ cm$，$AC\ =\ 6\ cm$，并且 $BC\ =\ 12\ cm$，求 $CE$ 的长度。

p>"\n

已知

在给定图形中，$AE$ 是外角 $∠\ CAD$ 的平分线，与 $BC$ 的延长线交于点 $E$。

$AB\ =\ 10\ cm$，$AC\ =\ 6\ cm$，并且 $BC\ =\ 12\ cm$。

要求

我们需要求出 $CE$ 的长度。

解答

$AE$ 是 $∠\ CAD$ 的平分线，这意味着：

$\angle BAD=\angle CAD$

我们知道：

三角形一个外角的平分线将对边外分，其比等于夹该角的两边的比。

因此：

$\frac{BE}{CE} = \frac{AB}{CA}$

$\frac{12+x}{x} = \frac{10}{6}$

$6(12+x) = 10(x)$

$72+6x = 10x$

$10x-6x=72$

$4x=72$

$x=\frac{72}{4}$

$x=18\ cm$

$CE$ 的长度为 $18\ cm$。  

教程点

更新于: 2022年10月10日

39 次浏览

开启你的 职业生涯

通过完成课程获得认证

立即开始