如图所示，证明 AB ∥ EF。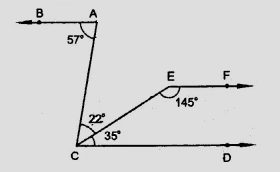

解题步骤

我们需要证明 AB ∥ EF。

解答

根据图形：

∠BAC = 57°，∠ACE = 22°

∠ECD = 35°，∠CEF = 145°

∠ECD + ∠CEF = 35° + 145°

= 180°

∠ECD 和 ∠CEF 是同旁内角。

因此：

EF ∥ CD

∠BAC = 57°

∠ACD = ∠ACE + ∠ECD

= 22° + 35°

= 57°

这意味着：

AB ∥ CD

EF ∥ CD 且 AB ∥ CD

因此：

AB ∥ EF。

证毕。

教程点

更新于：2022年10月10日

浏览量：65

开启你的职业生涯

完成课程获得认证

开始学习