数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会研究
服装研究
法律研究用图形方法证明以下每个方程组都有无穷多个解
2x + 3y = 6
4x + 6y = 12
已知
给定的方程组为
2x + 3y - 6 = 0
4x + 6y – 12 = 0
要求
我们必须证明上述方程组有无穷多个解。
解答
给定的方程组为
2x + 3y - 6 = 0....(i)
3y = 6 - 2x
y = (6 - 2x) / 3
4x + 6y - 12 = 0....(ii)
6y = 12 - 4x
y = (12 - 4x) / 6
为了用图形表示上述方程，我们需要每个方程至少两个解。
对于方程 (i)，
如果 x = 0，则 y = (6 - 2(0)) / 3 = 6 / 3 = 2
如果 x = 3，则 y = (6 - 2(3)) / 3 = (6 - 6) / 3 = 0 / 3 = 0
x | $0$ | $3$ |
y = (6 - 2x) / 3 | $2$ | $0$ |
对于方程 (ii)，
如果 x = 0，则 y = (12 - 4(0)) / 6 = 12 / 6 = 2
如果 x = 3，则 y = (12 - 4(3)) / 6 = (12 - 12) / 6 = 0 / 6 = 0
| x | $0$ | $3$ |
| y = (12 - 4x) / 6 | $2$ | $0$ |
上述情况可以用下图表示
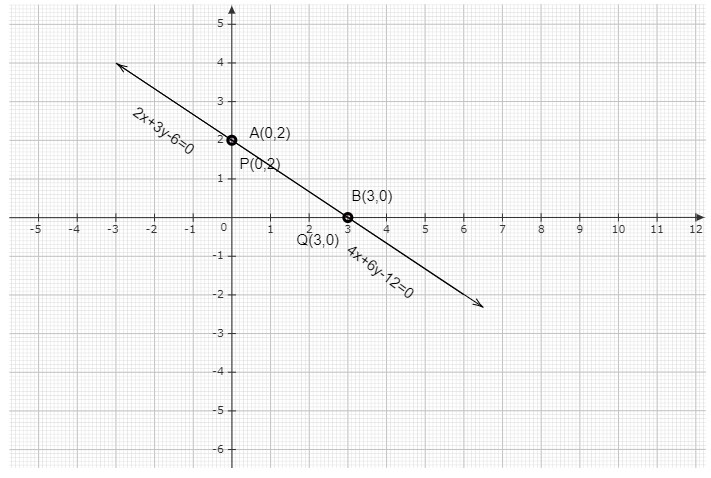
直线 AB 表示方程 2x + 3y - 6 = 0，直线 PQ 表示方程 4x + 6y - 12 = 0。
我们可以看到，两个方程表示同一条直线。
因此，给定的方程组有无穷多个解。
更新于：2022年10月10日
浏览量：55
广告