一个圆的两个弦$AB$和$CD$的长度分别为$5\ cm$和$11\ cm$，它们互相平行且位于圆心的异侧。如果$AB$和$CD$之间的距离为$6\ cm$，求圆的半径。

已知

圆的两个弦$AB$和$CD$的长度分别为$5\ cm$和$11\ cm$，它们互相平行且位于圆心的异侧。

$AB$和$CD$之间的距离为$6\ cm$。

要求

我们需要求出圆的半径。

解答

设圆的半径为$r$，圆心为$O$。

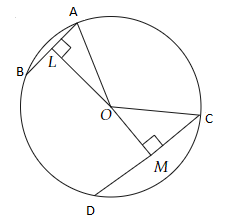
两个平行弦$AB = 5\ cm, CD = 11\ cm$

设$OL \perp AB$和$OM \perp CD$

$LM = 6\ cm$

设$OM = x$

这意味着，

$OL = 6 - x$

在直角三角形$\mathrm{OAL}$中，

$\mathrm{OA}^{2}=\mathrm{OL}^{2}+\mathrm{AL}^{2}$

$r^{2}=(6-x)^{2}+(\frac{5}{2})^{2}$

$=36-12 x+x^{2}+\frac{25}{4}$............(i)

类似地，

在直角$\Delta \mathrm{OCM}$中，

$r^{2}=x^{2}+(\frac{11}{2})^{2}$

$=x^{2}+\frac{121}{4}$..............(ii)

由(i)和(ii)，我们得到，

$x^{2}+\frac{121}{4}=36-12 x+x^{2}+\frac{25}{4}$

$\Rightarrow \frac{121}{4}-\frac{25}{4}-36=-12 x$

$\Rightarrow \frac{96}{4}-\frac{36}{1}=-12 x$

$\Rightarrow 12 x=36-24=12$

$x=\frac{12}{12}=1$

$\Rightarrow r^{2}=\mathrm{CM}^{2}+\mathrm{OM}^{2}$

$=(\frac{11}{2})^{2}+(1)^{2}$

$=\frac{121}{4}+1$

$=\frac{125}{4} \mathrm{~cm}$

$\Rightarrow r=\sqrt{\frac{125}{4}}$

$=\frac{\sqrt{125}}{2}$

$=\frac{\sqrt{25 \times 5}}{2}$

$=\frac{5}{2} \sqrt{5} \mathrm{~cm}$

圆的半径是$\frac{5}{2} \sqrt{5} \mathrm{~cm}$。

教程点

更新于: 2022年10月10日

67 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习