一条笔直的公路通往一座塔的底部。一个站在塔顶的人观察到一辆汽车，俯角为 $30^o$，这辆汽车以匀速驶近塔底。6秒后，发现汽车的俯角为 $60^o$。求从此时起汽车到达塔底所需的时间。

已知

一条笔直的公路通往一座塔的底部。

一个站在塔顶的人观察到一辆汽车，俯角为 $30^o$，这辆汽车以匀速驶近塔底。

6秒后，发现汽车的俯角为 $60^o$。

要求

我们需要求出从此时起汽车到达塔底所需的时间。

解答：  

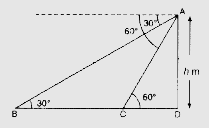
设公路为 $BCD$。

高为 $h$ 的塔位于点 $D$。

从塔顶点 $A$ 观察汽车的俯角为 $30^{\circ}$。

6 秒后，当汽车到达点 $C$ 时，俯角变为 $60^{\circ}$。

这意味着，

6 秒内汽车行驶的距离 = $\mathrm{BC}$

在直角三角形 $\mathrm{ADB}$ 中，

$\tan 30^{\circ}=\frac{\mathrm{AD}}{\mathrm{BD}}$

$\frac{1}{\sqrt{3}}=\frac{h}{BD}$

$BD=h \sqrt{3}$.............(i)

在直角三角形 $ADC$ 中，

$\tan 60^{\circ}=\frac{\mathrm{AD}}{\mathrm{CD}}$

$\sqrt{3}=\frac{h}{CD}$

$h=\sqrt{3}CD$.........(ii)

将 $h$ 的值代入 (i)，得到：

$BD=\sqrt{3}CD \times \sqrt{3}$

$=3 C D$

$BC+CD=3CD$

$3CD-CD=BC$

$2CD=BC$

$CD=\frac{1}{2} \mathrm{BC}$

行驶距离 $CD$ 所需的时间 = 行驶距离 $BC$ 所需时间的一半

$=\frac{1}{2} \times 6$

$=3$

因此，从此时起汽车到达塔底所需的时间为 3 秒。

教程点

更新于： 2022年10月10日

111 次查看

开启你的 职业生涯

完成课程获得认证

开始学习