已知:长方形草坪的尺寸为 50 米 × 40 米。池塘周围草坪的面积 = 1184 平方米。要求:我们需要找到池塘的长和宽。解:长方形草坪的面积 = 50 米 × 40 米 = 2000 平方米。池塘的面积 = 草坪的面积 - 草坪的面积池塘的面积 = (2000 - 1184) 平方米 = 816 平方米。设池塘周围草坪的宽度为 x 米。这意味着,池塘的长度 = 50 - 2x 米。池塘的宽度 = 40 - 2x 米。我们知道,长为 l,宽为 b 的矩形的面积为 lb。因此,长方形池塘的面积 = (50 - 2x)(40 - 2x) 平方米。根据题意,(50 - 2x)(40 - 2x) = 816 (来自公式 1)2000 - 100x - 80x + 4x^2 = 8164x^2 - 180x + 2000 - 816 = 04x^2 - 180x + 1184 = 04(x^2 - 45x + 296) = 0x^2 - 45x + 296 = 0求解 ... 阅读更多
要求:我们需要找到正确答案。解:将 x=2 代入 x^{2}-4 x+5 中,得到,(2)^{2}-4(2)+5=4-8+5=1 ≠ 0所以,x=2 不是 x^{2}-4 x+5=0 的根。将 x=2 代入 x^{2}+3 x-12 中,得到,(2)^{2}+3(2)-12=4+6-12=-2 ≠ 0所以,x=2 不是 x^{2}+3 x-12=0 的根。将 x=2 代入 2 x^{2}-7 x+6 中,得到,2(2)^{2}-7(2)+6 =2(4)-14+6=8-14+6=14-14=0所以,x=2 是方程 2 x^{2}-7 x+6=0 的根。将 x=2 代入 3 x^{2}-6 x-2 中,得到,3(2)^{2}-6(2)-2=12-12-2=-2 ≠ 0所以,x=2 不是 3 x^{2}-6 x-2=0 的根。阅读更多
要求:我们需要找到正确答案。解:2(x-1)^{2} =4 x^{2}-2 x+12(x^{2}+1-2 x) =4 x^{2}-2 x+12 x^{2}+2-4 x =4 x^{2}-2 x+12 x^{2}+2 x-1 =0它表示一个二次方程,因为它符合二次方程的形式 ax^{2}+bx+c=0, a ≠02 x-x^{2} =x^{2}+52 x^{2}-2 x+5 =0它也表示一个二次方程,因为它符合二次方程的形式 ax^{2}+bx+c=0, a ≠ 0.(\sqrt{2} x+\sqrt{3})^{2} =3 x^{2}-5 x2 x^{2}+3+2 \sqrt{6}x =3 x^{2}-5 x^{2}-(5+2 \sqrt{6}) x-3 =0它也表示一个二次方程,因为它符合二次方程的形式 ax^{2}+bx+c=0, a ≠ 0(x^{2}+2 x)^{2}=x^{4}+3+4 x^{2}x^{4}+4 x^{2}+4 x^{3} ... 阅读更多
要求:我们需要找到正确答案。解:将 x=2 代入 x^{2}-4 x+5 中,得到,(2)^{2}-4(2)+5=4-8+5=1 ≠ 0所以,x=2 不是 x^{2}-4 x+5=0 的根。将 x=2 代入 x^{2}+3 x-12 中,得到,(2)^{2}+3(2)-12=4+6-12=-2 ≠ 0所以,x=2 不是 x^{2}+3 x-12=0 的根。将 x=2 代入 2 x^{2}-7 x+6 中,得到,2(2)^{2}-7(2)+6 =2(4)-14+6=8-14+6=14-14=0所以,x=2 是方程 2 x^{2}-7 x+6=0 的根。将 x=2 代入 3 x^{2}-6 x-2 中,得到,3(2)^{2}-6(2)-2=12-12-2=-2 ≠ 0所以,x=2 不是 3 x^{2}-6 x-2=0 的根。
已知:\( \frac{1}{2} \) 是方程 \( x^{2}+k x-\frac{5}{4}=0 \) 的一个根。要求:我们需要找到 k 的值。解:$\frac{1}{2}$ 是二次方程 $x^{2}+k x-\frac{5}{4}=0$ 的一个根这意味着,$(\frac{1}{2})^{2}+k(\frac{1}{2})-\frac{5}{4}=0$$\frac{1}{4}+\frac{k}{2}-\frac{5}{4}=0$$\frac{1+2 k-5}{4}=0$$2 k-4=0$$2 k=4 $$k=2$k 的值为 2。
要求:我们需要找到正确答案。解:2 x^{2}-3 x+6=0与 ax^{2}+bx+c=0 比较,得到,a=2, b=-3 和 c=6根之和 = \frac{-b}{a}=\frac{-(-3)}{2}=\frac{3}{2}所以,二次方程 2 x^{2}-3 x+6=0 的根之和不等于 3.-x^{2}+3 x-3=0与 ax^{2}+bx+c=0 比较,得到,a=-1, b=3 和 c=-3根之和 = \frac{-3}{-1}=3所以,二次方程 -x^{2}+3 x-3=0 的根之和为 3.$\sqrt{2} x^{2}-\frac{3}{\sqrt{2}} x+1=0$$2 x^{2}-3 x+\sqrt{2}=0$与 ax^{2}+bx+c=0 比较,得到,a=2, b=-3 和 c=\sqrt{2}根之和 = \frac{-b}{a}=\frac{-(-3)}{2}=\frac{3}{2}所以,二次方程 $\sqrt{2} x^{2}-\frac{3}{\sqrt{2}} x+1=0$ 的根之和不等于 3.$3 x^{2}-3 x+3=0$$x^{2}-x+1=0$与 ... 阅读更多
要求:我们需要找到正确答案。解:$2 x^{2}-k x+k=0$与 $a x^{2}+b x+c=0$ 比较,得到,$a=2, b=-k$ 和 $c=k$我们知道,对于相等根,判别式必须为零。因此,$D=b^{2}-4 a c=0$$(-k)^{2}-4(2) k=0$$k^{2}-8 k=0$$k(k-8)=0$$k=0$ 或 $k=8$因此,k 的所需值为 0 和 8。
要求:我们需要找到正确答案。解:$9 x^{2}+\frac{3}{4} x-\sqrt{2}=0$$(3 x)^{2}+\frac{1}{4}(3 x)-\sqrt{2}=0$设 3x=k这意味着,$k^{2}+\frac{1}{4}k-\sqrt{2}=0$$k^{2}+\frac{1}{4}k+(\frac{1}{8})^{2}-(\frac{1}{8})^{2}-\sqrt{2}=0$$(k+\frac{1}{8})^{2} =\frac{1}{64}+\sqrt{2}$$(k+\frac{1}{8})^{2}=\frac{1+64\sqrt{2}}{64}$因此,$\frac{1}{64}$ 必须被添加和减去以求解给定方程。
要求:我们需要找到正确答案。解:$2 x^{2}-\sqrt{5} x+1=0$与 $a x^{2}+b x+c=0$ 比较,得到,$a=2, b=-\sqrt{5}$ 和 $c=1$因此,$D =b^{2}-4 a c$$=(-\sqrt{5})^{2}-4 \times(2) \times(1)$$=5-8$$=-3
要求:我们需要找到正确答案。解:$2 x^{2}-3 \sqrt{2} x+\frac{9}{4}=0$与 $a x^{2}+b x+c=0$ 比较,得到,a=2, b=-3 \sqrt{2} 和 c=\frac{9}{4}$$D=b^{2}-4 a c$$=(-3 \sqrt{2})^{2}-4(2)(\frac{9}{4})$$=18-18$$=0$所以,该方程有两个相等的实根。$x^{2}+x-5=0$与 $a x^{2}+b x+c=0$ 比较,得到,a=1, b=1 和 c=-5$$D=b^{2}-4 a c$$=(1)^{2}-4(1)(-5)$$=1+20$$=21>0$所以,$x^{2}+x-5=0$ 有两个不同的实根。$x^{2}+3 x+2 \sqrt{2}=0$与 $a x^{2}+b x+c=0$ 比较,得到,a=1, b=3 和 c=2 \sqrt{2}$$D=b^{2}-4 a c$$=(3)^{2}-4(1)(2 \sqrt{2})$$=9-8 \sqrt{2}阅读更多

 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP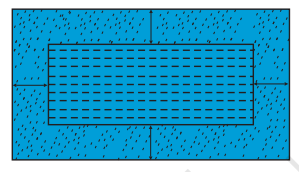 "
"
