数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
已知：在正方形的一边上作等边三角形。需要做：我们需要证明在正方形的一边上作等边三角形的面积等于在它的对角线上作等边三角形面积的一半。解：设正方形 ABCD 的边长为 a。这意味着，AC² = AB² + BC² = a² + a² = 2a² AC = √2a ∠PAD = ∠QAC = 60° ∠PDA = ∠QCA = 60° 因此，根据 AA 相似性，ΔPAD ~ ΔQAC 这意味着，ar(ΔPAD) / ar(ΔQAC) = AD² / AC² = a² / (√2a)² = 1/2 ar(ΔPAD) = 1/2(ar(ΔQAC)) 证毕。阅读更多
需要做：我们需要证明两个相似三角形的面积之比等于它们对应中线的平方之比。解：设ΔABC ~ ΔDEF。AP 和 DQ 是中线。我们知道，两个相似三角形的面积之比等于它们对应边的平方之比。这意味着，ar(ΔABC) / ar(ΔDEF) = AB² / DE² ΔABC ~ ΔDEF 这意味着，AB / DE = BC / EF = 2BP / 2EQ = BP / EQ AB / DE = BP / EQ ……(i) ∠B = ∠E (对应角) 因此，根据 SAS 准则，ΔABP ~ ΔDEQ 这意味着，BP / EQ = AP / DQ ……(ii) 从 (i) 和 (ii) 中，我们得到，AB / DE = AP / DQ 因此，ar(Δ... 阅读更多
已知：两个相似三角形的面积相等。需要做：我们需要证明它们全等。解：设ΔABC ~ ΔDEF，使得 ar(ΔABC) = ar(ΔDEF) ar(ΔABC) / ar(ΔDEF) = AB² / DE² = AC² / DF² = BC² / EF² 这意味着，AB² / DE² = AC² / DF² = BC² / EF² = 1 因此，AB² = DE² AB = DE AC² = DF² AC = DF BC² = EF² BC = EF 因此，根据 SSS 准则，ΔABC ≅ ΔDEF 阅读更多
已知：D、E 和 F 分别是△ABC 的边 AB、BC 和 CA 的中点。需要做：我们需要求△DEF 和△ABC 的面积之比。解：D 和 E 分别是边 AB 和 BC 的中点。我们知道，连接三角形两边中点的线段平行于第三边且等于第三边的一半。这意味着，EF = 1/2AB DF = 1/2BC DE = 1/2AC 因此，DE / AC = EF / AB = DF / BC = 1/2 因此，根据 SSS 准则，ΔDEF ~ ΔABC 这意味着，ar(ΔDEF) / ar(ΔABC) = DE² / AC² = (1/2)² = 1/4 △DEF 和△ABC 的面积之比为 1:4。阅读更多
"
已知：ABC 和 DBC 是同底 BC 上的两个三角形。AD 交 BC 于 O 需要做：我们需要证明\( ar(△ABC) / ar(△DBC) = AO / DO \) 解：作 AM ⊥ BC 和 DN ⊥ BC 在△AOM 和△DON 中，∠AOM = ∠DON (对顶角) ∠AMO = ∠DNO = 90° 因此，根据 AA 相似性，△AOM ~ △DON 这意味着，AM / DN = AO / DO (对应边成比例) 因此，ar(△ABC) / ar(△DBC) = (1/2 × BC × AM) / (1/2 × BC × DN) = AM / DN ar(△ABC) / ar(△DBC) = AO / DO (因为 AM / DN = AO / DO) 证毕。阅读更多
已知：两个三角形△ABC 和△PQR，其中△ABC 的边 AB、AC 和中线 AD 与△PQR 的边 PQ、PR 和中线 PM 成比例 AB / PQ = AC / PR = AD / PM 需要做：我们需要证明△ABC ~ △PQR 解：我们有，AB / PQ = AC / PR = AD / PM (D 是 BC 的中点，M 是 QR 的中点) △ABD ~ △PQM (SSS 相似性准则) 因此，∠ABD = ∠PQM (两个相似三角形的对应角相等) ∠ABC = ∠PQR 在△ABC 和△PQR 中 AB / PQ = AC / PR ……(i) ∠A = ∠P ……(ii) 从上述等式 (i) 和 (ii) 中，我们得到，△ABC ~ △PQR ... 阅读更多
已知：一根长 6 米的竖直杆投下 4 米长的阴影。一座塔投下 28 米长的阴影。需要做：我们需要求塔的高度。解：杆长 = 6 米。杆的阴影长度 = 4 米。塔的阴影长度 = 28 米。设塔的高度为 h 米。在△ABC 和△PQR 中 ∠ABC = ∠PQR = 90° ∠ACB = ∠PRQ (太阳高度角相同) 因此，△ABC ~ △PQR (根据 AA 相似性) 这意味着，AB / BC = PQ / QR (对应边成比例) 6 / 4 = h / 28 h = (28 × 6) / 4 h = ... 阅读更多
已知：AD 和 PM 分别是△ABC 和△PQR 的中线，其中△ABC ~ △PQR。需要做：我们需要证明 AB / PQ = AD / PM。解：已知△ABC ~ △PQR 我们知道，相似三角形的对应边成比例。这意味着，AB / PQ = AC / PR = BC / QR ……(i) ∠A = ∠P，∠B = ∠Q，∠C = ∠R ……(ii) AD 和 PM 是中线。这意味着，它们分别平分它们的对边 BC 和 QR。因此，BD = BC / 2 QM = QR / 2 ……(iii) 从等式 (i) 和 (iii) 中，我们得到，AB / PQ = BD / QM ……(iv) 在△ABD 和△PQM 中，∠B = ∠Q (对... 阅读更多
**已知：**设$∆ABC \sim ∆DEF$，它们的面积分别为$64\ cm^2$和$121\ cm^2$。$EF = 15.4\ cm$**求：**我们需要求出BC。**解：**我们知道，两个相似三角形的面积之比等于它们对应边平方之比。因此，$\frac{\operatorname{ar}(\triangle \mathrm{ABC})}{\operatorname{ar}(\Delta \mathrm{DEF})}=\frac{\mathrm{BC}^{2}}{\mathrm{EF}^{2}}$这意味着，$\frac{64}{121}=\frac{\mathrm{BC}^{2}}{(15.4)^{2}}$$\frac{8}{11}=\frac{\mathrm{BC}}{15.4}$$\mathrm{BC}=\frac{8 \times 15.4}{11}$$BC=11.2\ cm
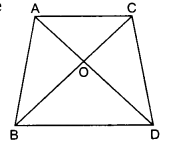
**已知：**梯形ABCD的对角线AC和BD交于点O，$AB \| DC$且$AB = 2 CD$。**求：**我们需要求出三角形AOB和COD的面积之比。**解：**在$\triangle \mathrm{AOB}$和$\triangle \mathrm{COD}$中，$\angle \mathrm{AOB} =\angle \mathrm{COD}$ (对顶角)$\angle 1=\angle 2$ (内错角)因此，根据AA相似，$\Delta \mathrm{AOB} \sim \Delta \mathrm{COD}$这意味着， $\frac{\operatorname{ar} \Delta \mathrm{AOB}}{\operatorname{ar} \Delta \mathrm{COD}}=\frac{\mathrm{AB}^{2}}{\mathrm{CD}^{2}}$$=\frac{(2 \mathrm{CD})^{2}}{\mathrm{CD}^{2}}$$=\frac{4 \mathrm{CD}^{2}}{\mathrm{CD}^{2}}$$=\frac{4}{1}$三角形AOB和COD的面积之比为$4:1$。 阅读更多