已知:在给定图形中,△ABC 的高 AD 和 CE 相交于点 P。 求证:(i) △AEP ∽ △CDP (ii) △ABD ∽ △CBE (iii) △AEP ∽ △ADB (iv) △PDC ∽ △BEC 证明:(i) 在△AEP 和△CDP 中,∠AEP = ∠CDP = 90°,∠APE = ∠CPD (对顶角)。因此,根据 AA 判定定理,△AEP ∽ △CDP。证毕。(ii) 在△ABD 和△CBE 中,∠ADB = ∠CEB = 90°,∠ABD = ∠CBE (公共角)。因此,根据 AA 判定定理,△ABD ∽ △CBE。证毕。(iii) 在△AEP 和△ADB 中,∠AEP = ∠… 阅读更多
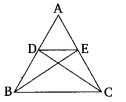
已知:△ABE ≅ △ACD 求证:△ADE ∽ △ABC 证明:△ABE ≅ △ACD,则 AB=AC,AE=AD (全等三角形的对应边相等)。因此,AB/AC=AD/AE=1。∠DAE=∠BAC。因此,根据 SAS 判定定理,△ADE ∽ △ABC。证毕。
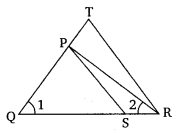
已知:S 和 T 分别是△PQR 的边 PR 和 QR 上的点,使得∠P = ∠RTS。 求证:△RPQ ∽ △RTS。 证明:在△RPQ 和△RTS 中,∠P = ∠RTS,∠P = ∠R。因此,根据 AA 判定定理,△RPQ ∽ △RTS。证毕。
已知:QR/QS = QT/PR 且∠1 = ∠2。 求证:△PQR ∽ △TQR。 证明:∠1 = ∠2,则 PQ = PR (等角对等边)。在△PQS 和△TQR 中,QR/QS = QT/PR,由于 PQ=PR,所以 QR/QS = QT/PQ。∠PQS = ∠TQR = ∠1。因此,根据 SAS 判定定理,△PQS ∽ △TQR。证毕。(注意:原证明中结论有误,这里修正为相似三角形为PQS和TQR)
已知:梯形 ABCD (AB∥DC) 的对角线 AC 和 BD 相交于点 O。 求证:OA/OC = OB/OD。 证明:在△AOB 和△COD 中,∠AOB = ∠COD (对顶角相等),∠OAB = ∠OCD (AB∥DC,内错角相等)。因此,△AOB ∽ △COD。则 OA/OC = OB/OD (相似三角形的对应边成比例)。证毕。
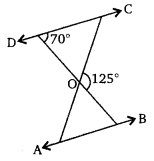
已知:△ODC ∽ △OBA,∠BOC = 125° 且∠CDO = 70°。 求∠DOC、∠DCO 和∠OAB。 解:由图可知,∠DOC = 180° - 125° = 55° (平角)。在△DOC 中,∠DCO + ∠ODC + ∠DOC = 180°,∠DCO + 70° + 55° = 180°,∠DCO = 55°。因为△ODC ∽ △OBA,所以∠OAB = ∠OCD = 55°。因此,∠DOC = 55°,∠DCO = 55°,∠OAB = 55°。
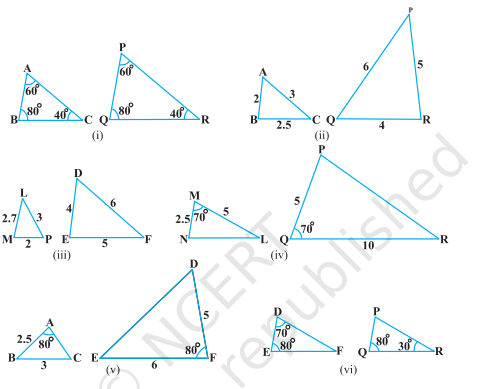
解:(i) 在△ABC 和△PQR 中,∠A = ∠P = 60°,∠B = ∠Q = 80°,∠C = ∠R = 40°。因此,根据 AAA 判定定理,△ABC ∽ △PQR。(ii) 在△ABC 和△PQR 中,BC/PR = 2.5/5 = 1/2,AB/QR = 2/4 = 1/2,AC/PQ = 3/6 = 1/2。因此,根据 SSS 判定定理,△ABC ∽ △QRP。(iii) 在△LMP 和△EFD 中,LM/EF = 2.7/5 = 27/50,LP/DF = 3/6 = 1/2,MP/DE = 2/4 = 1/2。LM/EF ≠ LP/DF = MP/DE,因此△LMP 与△EFD 不相似。(iv) 在△MNL 和△PQR 中,MN/PQ = 2.5/5 = 1/2,ML/QR = 5/10 = 1/2,∠M = ∠Q = 70°。因此,根据 SAS 判定定理,△NML ∽ △PQR。(v) … 阅读更多
已知:四边形 ABCD 的对角线相交于点 O,使得 AO/BO = CO/DO。 求证:ABCD 是梯形。 证明:作 EF∥AB。AO/BO = OC/OD,则 AO/CO = BO/DO……(i)。在△BAD 中,EO∥AB,根据比例线段定理,DE/EA = DO/BO,AE/ED = BO/DO……(ii)。由 (i) 和 (ii) 得,AO/CO = AE/ED。根据比例线段定理的逆定理,OE∥CD。因为 AB∥OE,所以 AB∥CD。因此,ABCD 是梯形。证毕。阅读更多
已知:ABCD 是一个梯形,其中 AB∥DC,其对角线相交于点 O。 求证:AO/BO = CO/DO。 证明:作 EO∥DC。在△ABD 中,DC∥AB,EO∥DC,则 AE/ED = BO/DO……(i)。在△ADC 中,EO∥DC,则 AE/ED = AO/CO……(ii)。由 (i) 和 (ii) 得,BO/DO = AO/CO,则 AO/BO = CO/DO。证毕。
证明:设在△ABC 中,D 为 AB 的中点。在△ABC 中,AD/DB = 1……(i),AE/EC = 1……(ii)。因此,AD/DB = AE/EC。根据比例线段定理的逆定理,DE∥BC。证毕。

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP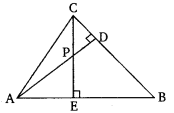 "
"

 "
"
 "
"
 "
"
 "
"