数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学
已知：D是三角形ABC的BC边上的一点，使得∠ADC = ∠BAC。 求证：CA² = CB·CD。证明：在△ABC和△DAC中，∠C=∠C (公共角)；∠BAC=∠ADC。因此，根据AA相似准则，△ABC ∽ △DAC。这意味着 CA/CD = CB/CA，所以CA²=CB × CD。证毕。
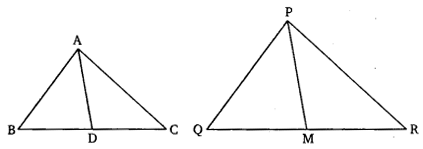
已知：三角形ABC的边AB和BC以及中线AD分别与三角形PQR的边PQ和QR以及中线PM成比例。求证：△ABC ∽ △PQR。证明：在△ABC和△PQR中，AB/PQ = BC/QR = AD/PM；AB/PQ = (1/2)BC/(1/2)QR = AD/PM；AB/PQ = BD/QM = AD/PM。因此，根据SSS相似准则，△ABD ∽ △PQM。这意味着∠B=∠Q (对应角相等)。在△ABC和△PQR中，∠B=∠Q，AB/PQ = BC/QR。因此，根据SAS相似准则，△ABC ∽ △PQR。阅读更多
"
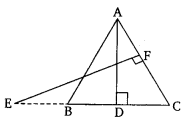
已知：E是等腰三角形ABC的CB边延长线上的一点，其中AB=AC；AD⊥BC且EF⊥AC。求证：△ABD ∽ △ECF。证明：△ABC是等腰三角形，AB=AC，这意味着∠ABC=∠ACB（等边对等角）。在△ABD和△ECF中，∠ABD=∠ECF（∠BCA=∠ECF）；∠ADB=∠EFC=90°。因此，根据AA相似准则，△ABD ∽ △ECF。证毕。
"
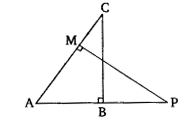
已知：ABC和AMP是两个直角三角形，分别在B和M处成直角。求证：△ABC ∽ △AMP。证明：在△ABC和△AMP中，∠B=∠AMP=90°；∠A=∠A（公共角）。因此，根据AA相似准则，△ABC ∽ △AMP。这意味着CA/PA = BC/MP (对应边成比例)。证毕。
已知：CD和GH分别是∠ACB和∠EGF的角平分线，D和H分别位于△ABC和△EFG的边AB和FE上；△ABC ∽ △FEG。求证：(i) CA/FG = CD/GH；(ii) △DCB ∽ △HGE；(iii) △DCA ∽ △HGF。证明：(i) △ABC ∽ △FEG，这意味着∠A=∠F，∠B=∠E，∠C=∠G，AB/FE=BC/EG=AC/FG。在△ACD和△FGH中，∠A=∠F，∠1=∠2（因为(1/2)∠C=(1/2)∠G）。因此，根据AA相似准则，△ACD ∽…阅读更多
"
已知：ABC和AMP是两个直角三角形，分别在B和M处成直角。求证：(i) △ABC ∽ △AMP；(ii) CA/PA = BC/MP。证明：(i) 在△ABC和△AMP中，∠B=∠AMP=90°；∠A=∠A（公共角）。因此，根据AA相似准则，△ABC ∽ △AMP。证毕。(ii) 在△ABC和△AMP中，∠B=∠AMP=90°；∠A=∠A（公共角）。因此，根据AA相似准则，△ABC ∽ △AMP。这意味着CA/PA = BC/MP (对应边成比例)。证毕。阅读更多
已知：E是平行四边形ABCD的边AD延长线上的一点，BE与CD相交于F。求证：△ABE ∽ △CFB。证明：在图中，ABCD是平行四边形，E是AD延长线上的一点，BE与CD相交于F。在平行四边形ABCD中，∠A=∠C (对角相等)。在△ABE和△CFB中，∠EAB=∠BCF (内错角相等)，∠ABE=∠BFC (内错角相等)。因此，根据AA相似准则，△ABE ∽ △CFB。证毕。
"
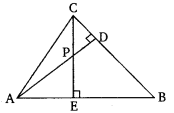
已知：在给定图形中，△ABC的高AD和CE相交于点P。求证：△PDC ∽ △BEC。证明：在△PDC和△BEC中，∠PDC=∠BEC=90°；∠PCD=∠BCE（公共角）。因此，根据AA相似准则，△PDC ∽ △BEC。证毕。
已知：在给定图形中，△ABC的高AD和CE相交于点P。求证：△AEP ∽ △ADB。证明：在△AEP和△ADB中，∠AEP=∠ADB=90°；∠A=∠A（公共角）。因此，根据AA相似准则，△AEP ∽ △ADB。证毕。
已知：在给定图形中，△ABC的高AD和CE相交于点P。求证：△ABD ∽ △CBE。证明：在△ABD和△CBE中，∠ADB=∠CEB=90°；∠ABD=∠CBE（公共角）。因此，根据AA相似准则，△ABD ∽ △CBE。证毕。