数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
已知：ABC 是一个等腰直角三角形，∠C=90°。要求：我们需要证明 $AB^2 = 2AC^2$。解答：在 ∆ABC 中，根据勾股定理，$AB^2= BC^2 + AC^2$$AB^2 = AC^2 + AC^2$$= 2AC^2$证毕。
已知：ABC 是一个等腰三角形，AC = BC 且 $AB^2 = 2AC^2$。要求：我们需要证明 ABC 是一个直角三角形。解答：在 ∆ABC 中，$AB^2 = 2AC^2$。$AB^2= AC^2 + AC^2$$AB^2 = AC^2 + BC^2$这意味着，根据勾股定理的逆定理，$\angle ACB= 90^o$因此，ABC 是一个直角三角形。证毕。
"
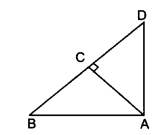
已知：△ABD 是一个直角三角形，∠A=90°，且 $AC \perp BD$。要求：我们需要证明 (i) $AB^2 = BC.BD$(ii) $AC^2 = BC.DC$(iii) $AD^2= BD.CD$解答：(i) 在 △ABD 和 △ABC 中，∠DAB=∠ACB=90°∠B=∠B (公共角)因此，△ADB ∽ △CAB (根据 AA 相似性)这意味着，$\frac{AB}{CB}=\frac{BD}{AB}$ (相似三角形对应边成比例)$AB.AB=CB.BD$ (交叉相乘)$AB^2=BC.BD$证毕。 (ii) 令∠CAB=x，这意味着，∠CAD=90°-x在 △CAB 中，∠CAB+∠BCA+∠ABC=180°$x+90°+∠ABC=180°$$∠ABC=180°-90°-x=90°-x在 △CAD 中，∠CAD+∠CDA+∠ADC=180°$90^-x+90°+∠ADC=180°$$∠ADC=180°-180°+x=x因此，在 △CAB 和 △CAD 中，∠CAB=∠ADC=x∠ABC=∠CAD=90°-x 因此，△CAB ∽ △CDA ... 阅读更多
已知：ABC 和 BDE 是两个等边三角形，D 是 BC 的中点。要求：我们需要找到 △ABC 和 △BDE 的面积之比。解答：在 △ABC 和 △ABC 中，∠A=∠E (△ABC 和 △BDE 是等边三角形)∠ABC=∠BED (△ABC 和 △BDE 是等边三角形)因此，△ABC ∽ △BDE (根据 AA 相似性)我们知道，如果两个三角形相似，则这两个三角形的面积之比与其对应边之比的平方成正比。因此，$\frac{ar(\triangle ABC)}{ar(\triangle BDE)}=\frac{BC^2}{BD^2}$$=\frac{(2BD)^2}{BD^2}$ (D 是 ... 阅读更多
已知：两个相似三角形的边长之比为 4:9。要求：我们需要找到这两个三角形的面积之比。解答：我们知道，如果两个三角形相似，则这两个三角形的面积之比与其对应边之比的平方成正比。因此，三角形面积之比 $=(\frac{4}{9})^{2}$$=\frac{16}{81}$给定三角形的面积之比为 16:81。
要求：我们需要确定三角形是否是直角三角形，并在每种情况下写出其斜边的长度。解答：(i) 令 $a=7\ cm$，$b=24\ cm$ 和 $c=25\ cm$。我们知道，如果斜边的平方等于其他两边的平方和，则该三角形是直角三角形。 因此，$(a)^2=(7\ cm)^2=49\ cm^2$$(b)^2=(24\ cm)^2=576\ cm^2$$(c)^2=(25\ cm)^2=625\ cm^2$这里，$(a)^2+(b)^2=(49+576)\ cm^2=625\ cm^2$$(a)^2+(b)^2=(c)^2$因此，根据勾股定理的逆定理，给定的边是直角三角形的边。 斜边的长度为 25 厘米。(ii) 令 $a=3\ cm$，$b=8\ cm$ 和 $c=6\ cm$。我们知 ... 阅读更多
已知：三角形的边长为 3 厘米、8 厘米和 6 厘米。要求：我们需要确定三角形是否是直角三角形，并写出其斜边的长度。解答：令 $a=3\ cm$，$b=8\ cm$ 和 $c=6\ cm$。我们知道，如果斜边的平方等于其他两边的平方和，则该三角形是直角三角形。 因此，$(a)^2=(3\ cm)^2=9\ cm^2$$(b)^2=(8\ cm)^2=64\ cm^2$$(c)^2=(6\ cm)^2=36\ cm^2$这里，$(a)^2+(c)^2=(9+36)\ cm^2=45\ cm^2$$(a)^2+(c)^2≠(b)^2$较长边的平方不等于其他两边的平方和。因此，给定的三角形不是直角三角形。阅读更多
已知：三角形的边长为 50 厘米、80 厘米和 100 厘米。要求：我们需要确定三角形是否是直角三角形，并写出其斜边的长度。解答：令 $a=50\ cm$，$b=80\ cm$ 和 $c=100\ cm$。我们知道，如果斜边的平方等于其他两边的平方和，则该三角形是直角三角形。 因此，$(a)^2=(50\ cm)^2=2500\ cm^2$$(b)^2=(80\ cm)^2=6400\ cm^2$$(c)^2=(100\ cm)^2=10000\ cm^2$这里，$(a)^2+(b)^2=(2500+6400)\ cm^2=8900\ cm^2$$(a)^2+(b)^2≠(c)^2$较长边的平方不等于其他两边的平方和。因此，给定的三角形不是直角三角形。阅读更多
**已知：**三角形的三条边分别为$a=13\ cm, b=12\ cm$和$c=5\ cm$。**求解：**我们需要确定这个三角形是否为直角三角形。**解答：**$a=13\ cm$$b=12\ cm$$c=5\ cm$我们知道，如果斜边的平方等于其他两条边的平方和，那么这个三角形就是直角三角形。因此，$(a)^2=(13\ cm)^2=169\ cm^2$$(b)^2=(12\ cm)^2=144\ cm^2$$(c)^2=(5\ cm)^2=25\ cm^2$这里，$(b)^2+(c)^2=(144+25)\ cm^2=169\ cm^2$$(b)^2+(c)^2=(a)^2$因此，根据勾股定理的逆定理，给定的边是直角三角形的边。斜边的长度为$13\ cm$。阅读更多
"
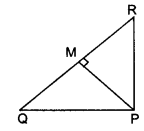
**已知：**PQR是一个直角三角形，∠P为直角，M是QR上一点，且$PM \perp QR$。**求解：**我们需要证明$PM^2 = QM • MR$。**解答：**在直角三角形PQR中，$\angle P = 90^o$$PM \perp QR$在$\triangle \mathrm{PMR}$中，根据勾股定理$(\mathrm{PR})^{2}=(\mathrm{PM})^{2}+(\mathrm{RM})^{2}$..........(i)在$\triangle \mathrm{PMQ}$中，根据勾股定理，$(PQ)^{2}=(P M)^{2}+(M Q)^{2}$..........(ii)在$\triangle \mathrm{PQR}$中，根据勾股定理，$(R Q)^{2}=(R P)^{2}+(P Q)^{2}$............(iii)因此，$(RM+MQ)^{2}=(R P)^{2}+(P Q)^{2}$$(R M)^{2}+(M Q)^{2}+2 R M . M Q=(R P)^{2}+(P Q)^{2}$.........(iv)将(i)和(ii)相加，得到$(\mathrm{PR})^{2}+(\mathrm{PQ})^{2}=2(\mathrm{PM})^{2}+(\mathrm{RM})^{2}+(\mathrm{MQ})^{2}$.........(v)从(iv)和(v)中，得到，$2 \mathrm{RM} . \mathrm{MQ}=2(\mathrm{PM})^{2}$$(\mathrm{PM})^{2}=\mathrm{RM} . \mathrm{MQ}$证毕。阅读更多