数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法学
已知：一个正圆锥的底面直径为 20 cm，顶面直径为 12 cm，高为 3 cm。求解：求其表面积和体积。解答：底面直径 = 20 cm，则底面半径 r₁ = 10 cm；顶面直径 = 12 cm，则顶面半径 r₂ = 6 cm；高 h = 3 cm。母线 l = √(h² + (r₁ - r₂)²) = √(3² + 4²) = 5 cm。总表面积 = π(r₁ + r₂)l + πr₁² + πr₂² = 80π + 100π + 36π = 216π ≈ 678.85 cm²。体积 = (π/3)(r₁² + r₁r₂ + r₂²)h = (π/3)(100 + 60 + 36) × 3 = 196π ≈ 615.75 cm³。阅读更多
已知：圆锥形台体的母线长为 4 cm，其圆形底面的周长分别为 18 cm 和 6 cm。求解：求其侧面积。解答：顶面周长 = 18 cm，则顶面半径 r₁ = 18/(2π) = 9/π cm；底面周长 = 6 cm，则底面半径 r₂ = 6/(2π) = 3/π cm；母线 l = 4 cm。侧面积 = π(r₁ + r₂)l = π(9/π + 3/π) × 4 = 48 cm²。阅读更多
已知：一个正圆锥形台体的底面周长分别为 44 cm 和 33 cm。台体的高为 16 cm。求解：求其体积、侧面积和总表面积。解答：顶面周长 = 44 cm，则顶面半径 r₁ = 7 cm；底面周长 = 33 cm，则底面半径 r₂ = 21/4 cm；高 h = 16 cm。母线 l = √(h² + (r₁ - r₂)²) ... 阅读更多
已知：一个高为 45 cm 的圆锥形桶，其底面半径分别为 28 cm 和 7 cm。求解：求此桶的容积。解答：设圆锥形桶的上半径 r₁ = 28 cm，下半径 r₂ = 7 cm，高 h = 45 cm。体积（容积）= (π/3)(r₁² + r₁r₂ + r₂²)h = (22/(7×3))[(28)² + 28×7 + (7)²] × 45 = 48510 cm³。
已知：一个圆锥的高为 20 cm。用平行于底面的平面从顶部切下一个小圆锥。小圆锥的体积是大圆锥体积的 1/125。求解：确定截面距底部的距离。解答：设大圆锥高 H = 20 cm，小圆锥高为 h₂。则剩余圆锥（台体）高 h₁ = 20 - h₂ cm。设大圆锥半径为 r₁，小圆锥半径为 r₂。则大圆锥体积 = (1/3)πr₁²H ... 阅读更多
已知：一个高为 24 cm 的水桶，其底面半径分别为 5 cm 和 15 cm。求解：求其表面积。解答：水桶（台体）高 h = 24 cm；上底半径 r₁ = 15 cm；下底半径 r₂ = 5 cm。母线 l = √(h² + (r₁ - r₂)²)= √(24² + 10²) = 26 cm。总表面积 = π(r₁ + r₂)l + πr₂² = 545π cm²。阅读更多
解：已知温度 = 25℃。使用公式 F = 32 + (9/5)C，则 25℃ = 32 + (9/5) × 25 = 77℉。
匀加速运动的速率-时间图可用于推导三个运动方程。考虑一个匀加速运动物体的速率-时间图。物体在 A 点具有初速度 'u'，然后在时间 't' 内其速度从 A 到 B 匀速变化。换句话说，从 A 到 B 有一个匀加速，经过时间 't' 后，其末速度变为 'v'，在图中等于 BC。时间 't' 由 OC 表示。为了完成该图，从点 C 作垂直线 CB，并从 A 点作平行于 OC 的垂直线 AD。从 B 点作垂直线 BE ... 阅读更多
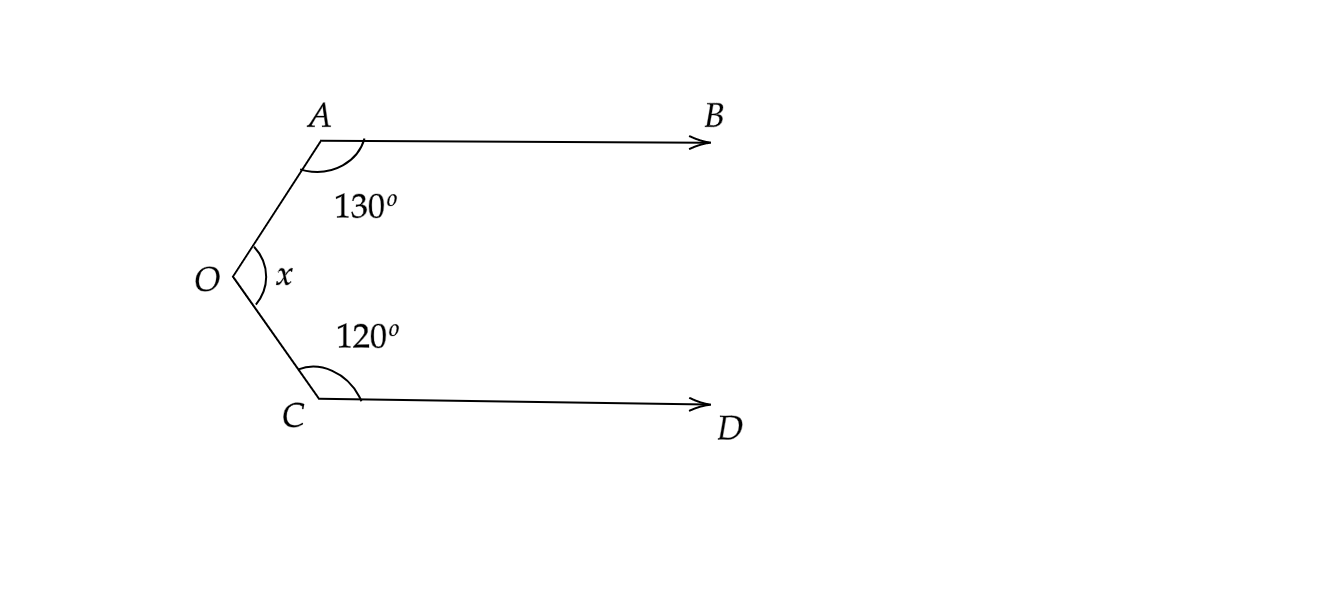
"\待求：在给定图中求x的值。解：连接AB。如图所示，AB∥CD，因此，∠BAC=∠ACD=90°。在△AOC中，∠OAC=∠OAB-∠BAC = 130°-90°=40°，∠OCA=∠OCD-∠DAC = 120°-90°=30°。因此，∠AOC+∠OAC+∠OCA=180° [三角形内角和为180°] ⇒ x+40°+30°=180° ⇒ x+70°=180° ⇒ x=180°-70° ⇒ x=110° 因此，x的值为110°。
已知：小球的初速度，u=0；下落距离或高度，s=20m；向下加速度，a=10ms⁻²；待求：小球撞击地面的最终速度(v)和小球撞击地面所需的时间(t)。解：假设小球撞击地面的最终速度为‘v’，撞击地面所需的时间为‘t’。根据运动学第三公式，我们知道：v²=u²+2as 代入已知值，我们得到：v²=0²+2×10×20 v²=0+400 v²=400 √v²=√400 v=20m/s 因此，小球撞击地面的最终速度为20m/s。现在，... 阅读更多